十、多節理岩石隧道穩定分析
多節理岩石隧道穩定分析與一般岩坡穩定分析方法步驟,大致相同,在此要提醒讀者是:『岩石隧道滑動體積大小,頂部滑動是受隧道寬部(跨度)控制;側壁則受隧道高跨度限制』。
如圖10.3之四方形隧道平面,平面i之三度空間平面方程式可以下列方式定義,即a![]() x+a
x+a![]() y+a
y+a![]() z=a
z=a![]() (i=1,n)…………(10.1),
(i=1,n)…………(10.1),
圖10.3中假定平面1~3(J1~J3)為岩層之不連續面;平面4(T1)為隧道右側平面;平面5(T2)為坑頂平面;平面6(T3)為隧道左側平面;平面7(T4)為隧道底盤平面,則平面1、2、5(i=1,2,5)之交點為A[x![]() ,y
,y![]() ,z
,z![]() ],平面2、3、5之交點為B[x
],平面2、3、5之交點為B[x![]() ,y
,y![]() ,z
,z![]() ],平面1、3、5之交點為C[x
],平面1、3、5之交點為C[x![]() ,y
,y![]() ,z
,z![]() ],平面1、2、3之交點為O[x
],平面1、2、3之交點為O[x![]() ,y
,y![]() ,z
,z![]() ],平面1、2、4之交點為P[x
],平面1、2、4之交點為P[x![]() ,y
,y![]() ,z
,z![]() ],平面2、3、4之交點為Q[x
],平面2、3、4之交點為Q[x![]() ,y
,y![]() ,z
,z![]() ],平面1、3、4之交點為R[x
],平面1、3、4之交點為R[x![]() ,y
,y![]() ,z
,z![]() ]……。如各平面之交點求出後,岩楔之表面積及體積可利用向量之叉積及三重積求解。岩楔之穩定問題可由各交點座標相對關係判定,而滑動模式可藉岩楔在滑動線兩側平面法線分力之計算值決定。
]……。如各平面之交點求出後,岩楔之表面積及體積可利用向量之叉積及三重積求解。岩楔之穩定問題可由各交點座標相對關係判定,而滑動模式可藉岩楔在滑動線兩側平面法線分力之計算值決定。
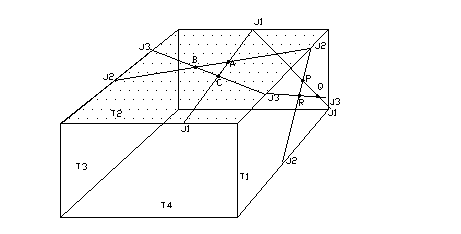
圖10.3隧道斷面示意圖
[例題10.1】:
如圖E10.1.1之隧道,三組節理J1:235/50,J2:010/50,J3:085/80均通過(0,0,-17.5)座標點,試評估分析其穩定情況?
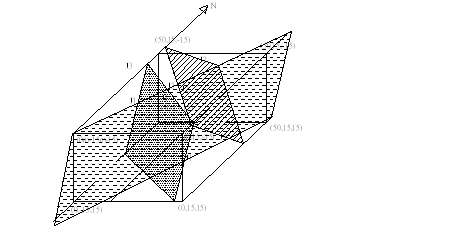
E10.1.1隧道斷面及節理關係示意圖
【解答】:
(1) 圖E10.1.2(a)為三組節理之等角度投影圖,(b)為垂直於隧道方向且經過岩楔頂
點之斷面示意圖。
(2) 節理J1:235/50之單位向上法線向量為[-.043938, -.062751, -.064279],因其通過
(0,0,-17.5),故其平面方程式為:
-0.43938x -0.62751y -0.64279z=11.24878……………(eq.1),節理J2及J3分別為:0.08583x+0 .98106y -0.17365z= 3.03884……………(eq.2),0.75441x+0.13302y-0.64279z=11.24878……………….(eq.3),右側平面(T1)、隧道頂(T2)、左側(T3)、及底盤(T4)分別為:y=15.0………………(eq4)
z=-15.0……………(eq.5),y=-15.0……………(eq.6),
及z=15.0……………………(eq.7)。
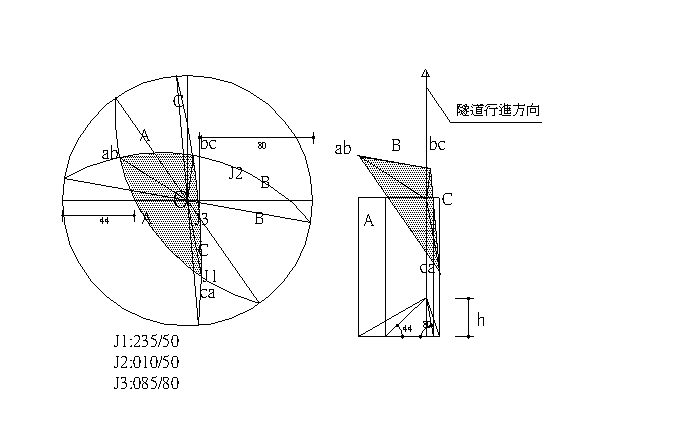 圖E10.1.2節理等角度投影及斷面示意圖
圖E10.1.2節理等角度投影及斷面示意圖
(3) 解方程式可得交點P(-9.55606,15.0, -25.61126 ),Q(120.17330,15.0 ,126.64530),
R(-84.38184,15.0,25.53679),O(0.0,0.0,-17.5),A(2.94531,
-4.62321,-15.0),B(2.08424,0.26015,-15.0),C(-4.90173,0.87135,
-15.0),P’(9.55605 ,-15.0,-9.38874),Q’(-120.17330,-15.0,
-161.64530),R’(84.38182,-15.0,-60.53677),A’(38.28898,
-60.10165,15.0),B’(27.09510,3.38200,15.00),C’(-63.72247,
11.32751,15.0)。
(4) O點座標在隧道中央頂部上面2.5公尺,岩楔四面體◇OABC之頂點O在底部三角形△ABC之上方,且底部△ABC各邊之長度均小於隧道之跨度,故岩楔◇OABC會因自重而墜落;岩楔◇OPQR及OP’Q’R,其底部△PQR或P’Q’R’各稜邊多大於隧道高度,因此無產生滑動之安全顧慮。
(5)岩楔◇OABC高為[2.94531,-4.62321,2.5].[0,0,1]=2.5公尺,◇OPQR及
OP’Q’R’高為15.0公尺,△OAB之面積為OA、OB兩向量叉積大小絕對值之半,即=15.631m![]() ,△OBC之面積為8.901m
,△OBC之面積為8.901m![]() ,△OCA之面積為8.901m
,△OCA之面積為8.901m![]() ,△ABC之面積為16.794m
,△ABC之面積為16.794m![]() ,◇OABC之體積為=13.995m
,◇OABC之體積為=13.995m![]() 。
。
【例題10.2】:
如圖E10.1.2之隧道,三組節理同例題10.1,但隧道方向非指北方向,為由南偏西70°指向北偏東70°,由地質調查資料顯示:J1節理通過(23.646,42.475,1.0),J2節理通過(9.268,42.475,1.0),J3節理通過(91.814,42.475,1.0)等座標點,試評估分析其穩定情況?
【解答】:
(1)三組節理之等角度投影圖同圖E10.1.2(a),圖E10.2.1 為隧道斷面及節理關係示意圖。
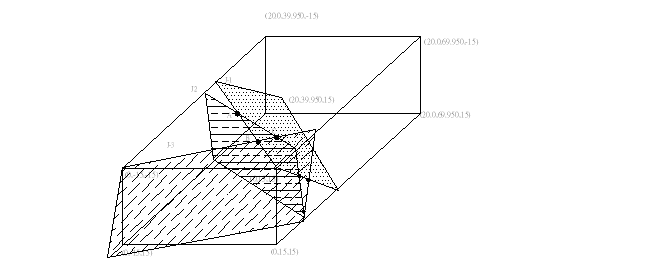 E10.2.1隧道斷面及節理關係示意圖
E10.2.1隧道斷面及節理關係示意圖
(3)比照例題10.1解方程式可得交點P(11.5676,47.0302,4.7477 ), Q(12.5676,49.5276,1.6859),R(12.8932,50.4239,6.8997),O(9.7462,50.0311,3.1249),A(-11.6072,83.5492,-15.0),B(45.2835,43.7139,-15.0),C(-5.3645,48.1450,-15.0),P’(18.6069,36.1225,10.6460),Q’(22.8231,47.7065,-3.5447),R’(24.3319,51.8517,20.6201),A’(23.7365,28.0707,15.0),B’(-13.5372,54.1701,15.0),及C’(19.6464,51.2669,15.0)。
(4)O點座標位置在隧道(T1)右側後方8.254m (50.0311-41.7774),岩楔◇OABC之頂點O在底部△ABC之下方,故岩楔◇OABC不會因自重而墜落;岩楔◇OP’Q’R’因開挖時已大部份移除,因此無產生滑動之安全顧慮;岩楔◇OPQR底部△PQR各稜邊多小於隧道高度,故有產生滑動之安全顧慮,因R點位置最低,故右側岩楔◇OPQR可能是沿OR(J2及J3)交線之楔型滑動破壞,或沿平面J2或J3之平面滑動。
(5)△OPR面積=7.930m![]() ,△OQR面積=7.736m
,△OQR面積=7.736m![]() ,◇OABC之體積為=7.895m
,◇OABC之體積為=7.895m![]() 。
。
(6)進一步分析發現岩楔在平面J3法線分力為負值,故岩楔◇OPQR沿平面J2滑動。如J2之凝聚力為0.5t/
m![]() ,摩擦角為30°時,安全係數為1.25,如不考慮凝聚力時安全係數為0.48(tan30°/tan50°)。
,摩擦角為30°時,安全係數為1.25,如不考慮凝聚力時安全係數為0.48(tan30°/tan50°)。
[例題10.3]:
在一個有三個不連續面存在之隧道開挖設計工程:平面PL-1之傾向及傾角為(235/45);PL-2之傾向及傾角為(125/45);PL-3之傾向及傾角為(000/45),三個不連續面岩層之內摩擦角![]() 均為30d,粘聚力C均為0.00t/m
均為30d,粘聚力C均為0.00t/m![]() ,岩石之單位重量為2.70t/m
,岩石之單位重量為2.70t/m![]() 。開挖後側壁平面之傾向/傾角為(170/90,不是外伸坡),隧道中心線之走向及傾角為080/45,隧道高度H=10.0m,試分析檢討其穩定情況?
。開挖後側壁平面之傾向/傾角為(170/90,不是外伸坡),隧道中心線之走向及傾角為080/45,隧道高度H=10.0m,試分析檢討其穩定情況?
[解答]:
(1)計算岩楔各邊之面積、體積及重量
(a)參考圖E10.3.1可得平面聯立方程如下
-0.4056x-0.5792y-0.7071z=d![]() ,-0.4092x+5792y-0.7071z=d
,-0.4092x+5792y-0.7071z=d![]()
0.7071x+0.0000y-0.7071z=d![]() ,-1.0000x+0.0000y+0.0000z=
d
,-1.0000x+0.0000y+0.0000z=
d![]()
(b)如令PL-1、PL-2及PL-3三不連續面之交點
 圖E10.3.1楔型滑動破壞示意圖
圖E10.3.1楔型滑動破壞示意圖
P![]() (x
(x![]() ,y
,y![]() ,z
,z![]() )=
P
)=
P![]() (0.0000,0.0000,0.0000)
,代入其對應之平面方程式求得各頂點座標,並依據已知條件修正後,得各點之正確座標為
(0.0000,0.0000,0.0000)
,代入其對應之平面方程式求得各頂點座標,並依據已知條件修正後,得各點之正確座標為
P![]() (0.0000,0.0000,0.0000),
P
(0.0000,0.0000,0.0000),
P![]() (-3.8835,0.0000,2.2275)
(-3.8835,0.0000,2.2275)
P![]() (-2.9009,5.5726,-2.9009),P
(-2.9009,5.5726,-2.9009),P![]() (-5.8727,-11.2814,-5.8727)
(-5.8727,-11.2814,-5.8727)
(2)岩楔之穩定判定:
觀察岩楔各頂點座標發現P![]() 點之座標z值為正,且大於P
點之座標z值為正,且大於P![]() 點之z值,而P
點之z值,而P![]() 、
P
、
P![]() 點之座標z值為負,故P
點之座標z值為負,故P![]() 在P
在P![]() 之下方,而P
之下方,而P![]() 、
P
、
P![]() 點在P
點在P![]() 之上方。故岩楔較有可能沿P
之上方。故岩楔較有可能沿P![]() P
P![]() 方向滑動,即由P
方向滑動,即由P![]() 向P
向P![]() 滑動。圖E10.3.3為岩楔在x-y平面投影圖,P
滑動。圖E10.3.3為岩楔在x-y平面投影圖,P![]() 在下故為非外伸坡無誤。
在下故為非外伸坡無誤。
岩楔各邊之面積及岩楔之體積: A![]() =15.303
m
=15.303
m![]() ,
,
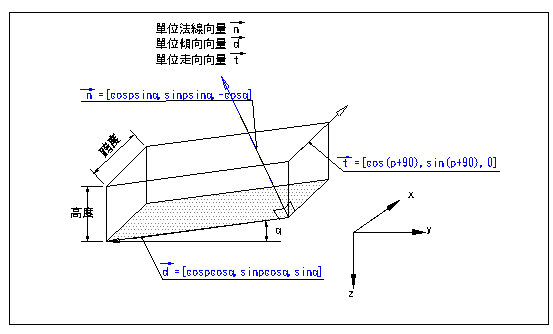 圖E10.3.2隧道高度、跨度與不連續面關係示意圖
圖E10.3.2隧道高度、跨度與不連續面關係示意圖
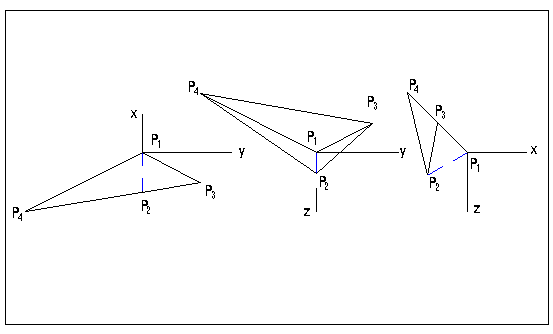 圖E10.3x-y,y-z,x-z投影圖
圖E10.3x-y,y-z,x-z投影圖
A![]() =30.979m
=30.979m![]() ,岩楔1-2-3-4體積,為P
,岩楔1-2-3-4體積,為P![]() 頂點,P
頂點,P![]() P
P![]() 、
P
、
P![]() P
P![]() 及
P
及
P![]() P
P![]() 為稜邊之岩楔體積,V=66.66m
為稜邊之岩楔體積,V=66.66m![]()
岩楔之重量W=66.66×2.70=180.00 t,i.e W=[0.00,0.00,180.00]
h![]() =(0.000+2.2275)/2=1.1137m
=(0.000+2.2275)/2=1.1137m
U![]() =
=![]() h
h![]() A
A![]() /3=1.0.1.1137.15.303/3=5.681t,
/3=1.0.1.1137.15.303/3=5.681t,
即U![]() =
5.681[-0.4056, -0.5792, -0.7071 ]
=
5.681[-0.4056, -0.5792, -0.7071 ]
U![]() =
=![]() h
h![]() A
A![]() /3=11.501t,
/3=11.501t,
即U![]() ==
11.501[ -0.4056,0 .5792, -0.7071 ]
==
11.501[ -0.4056,0 .5792, -0.7071 ]
(3)安全係數計算
case (a): 常時無地震及地下水
R=W=[0.00,0.00,180.00]
![]()
![]() 之單位向量為
[-0.8674,0.000,0.4795],故W沿
之單位向量為
[-0.8674,0.000,0.4795],故W沿![]()
![]() 滑動方向之分
滑動方向之分
力T之大小T,為[0.00,0.00,180.00]•[-0.8674,0.000,0.4975]=89.55
t,即T=89.55[-0.8674,0.000,0.4795]=[-77.6757,0.000,42.9392],如假定垂直於![]()
![]() 之W分向量為N,則
之W分向量為N,則
N=W-T=[74.86,0.00,138.61] ,如假設N在不連續平面PL-1及PL-2單位法線n![]() 及n
及n![]() 之分量為N
之分量為N![]() 及N
及N![]() ,即N
,即N![]() n
n![]() +N
+N![]() n
n![]() =
N ,i.e
=
N ,i.e
N![]() [0.4056,0.5792,0.7071]+N
[0.4056,0.5792,0.7071]+N![]() [0.4056,-5792,0.7071]=
[0.4056,-5792,0.7071]=
[77.68,0.00,137.06],故解出 N![]() =
N
=
N![]() =95.77
t
=95.77
t
抵抗滑動之抗力=c![]() A
A![]() +c
+c![]() A
A![]() +
N
+
N![]() tan(
tan(![]()
![]() )+N
)+N![]() tan(
tan(![]()
![]() )
)
=0.00+0.00+95.77•0.5774+95.77•0.5774=110.58
安全係數Fs= F![]() /F
/F![]() =110.58/89.55=1.235
=110.58/89.55=1.235
(4)有關其餘計算請參考例題10.1及10.2。
[例題10.4]:
除岩楔PL-3為外伸坡外,其餘同例題10.3,試分析檢討其穩定情況?
[解答]:
(1).同例題10.3,解法相同,因為PL-3為外伸坡,故岩楔之座標值與例題10.2比較,絕對值相同但符號相反。圖E10.4.1為岩楔在x-y平面上之投影,因PL-3為外伸故取上半部,即
P![]() 、P
、P![]() 在上,P
在上,P![]() 、P
、P![]() 在下。由相對座標值研判,岩楔係沿PL-3傾向方向滑動。
在下。由相對座標值研判,岩楔係沿PL-3傾向方向滑動。
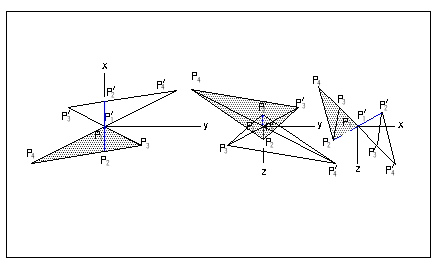
圖E10.4.1x-y,y-z,x-z投影圖