空間平面與岩楔座標、面積及體積計算

(空間平面研究系列之九)

一、前言

有關岩楔之稜線長度、面積、體積及各頂點之相對位置或煤層隱藏量估算等之求解，一般教科書或報告，多藉球體投影或正交投影方式，以圖解法或利用數學向量法求解。作圖法過程繁複費時，不適合電腦程式設計；向量解法及聯立方程式解法，比較適合電腦作業，其可提供計算者岩楔之相對位置關係。聯立方程式解法比向量解法更簡單明瞭，觀念更為直接，對初學者而言，應該比較容易接受及理解，另外如切割岩楔之平面數超過5個以上時，則向量解法就可能出現問題，因為切割後之岩塊立體圖示很難具體呈現及判斷其正確性。而聯立方程式解法如透過適當之編號程序及指令，電腦能自動並且正確地解出岩楔頂端座標及形狀，因此作者特別推介聯立方程式解法，提供讀者另類選擇。岩楔穩定分析，在岩體體積、滑動面接觸面積、滑動線、水壓力(推力及上舉力)及其他作用力已知後，相關力學分析與岩層平面滑動並無太大差異，因此本報告將偏重岩楔幾何性質的討論，至於力學分析部份則不作太多著墨。通常組成岩楔平面多以位態及關鍵性稜線尺寸或其長度分量定義岩體幾何性質，而野外用地質羅盤量測位態，受限於儀器底盤大小及量測習慣，因此精確度偏低，因此如能用較精密的測量儀器觀測點的3D座標，經適度調整，應能取得較正確的岩楔幾何資料，因此，本報告除介紹傳統的以位態及關鍵性稜線尺寸定義岩楔外，另討論如何以裸露岩楔座標計算岩楔座標以外的幾何性質。    

二、岩楔頂點編碼

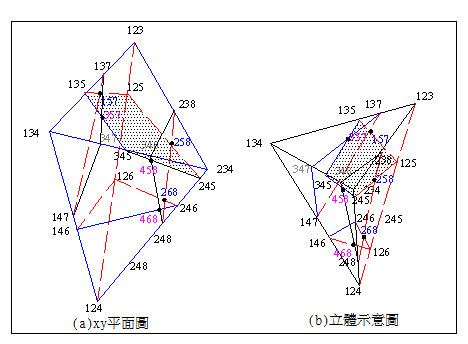
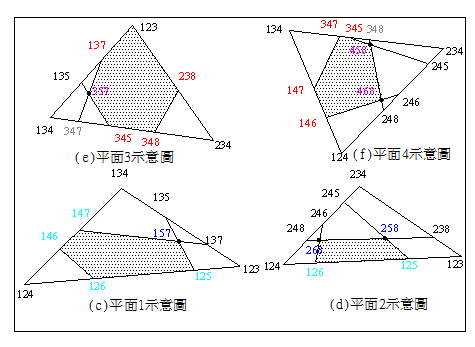
岩楔由4或5個平面所切割者，前者最多有個交點，後者最多有= =10交點；至於7或8個平面所切割者，則理論上最多有個交點，及交點，不要說是35個已經夠嚇人及複雜，更遑論56個者。7或8面體在空間所組成之幾何性質(頂端座標、稜線長、面積體積)計算，是可以作圖法或向量求解，但岩楔圖像繪製及溝通就會發生問題，答案之檢核也相當困難。此為一般教科書只討論4或5面體而不討論7或8面體之原因所在。在八面岩楔穩定分析電腦程式設計，岩楔頂點代號編碼關係程式之作業效率及圖像繪製至大，如任兩張力裂縫平面間不重疊時，可採用如點A或1(平面1、2及3交點)、B或點2(平面1、2及4交點)……方式，有重疊時則建議採用如123(平面1、2及3交點)、124……等，如超過10面時可採用1-2-3、1-2-11或_1_2_3、1_2_3或1_2_11等方式。根據筆者之經驗以採用1-2-3、或_1_2_3之編碼方式最為簡便，以圖2.1之八面體編碼方式而言，各岩楔頂點交點號碼可以很清楚找出相關之節理平面，各平面上之交點3個編碼中必須含1個與節理平面代碼相同之編號，如圖2.1(a)中之所有交點編號都必須有1，而相鄰之任兩交點連線(即2平面之交線)必須有2碼相同，不相鄰之兩交點至多有1碼相同，……。利用此特性可以很容易找出岩層經過切割後之正確岩楔關係，切割次數亦多亦能顯示此編碼方式之優越性。                

圖2.1八面體頂點編碼示意圖

三、岩楔幾何性質

兩平面交線可利用等角度投影作圖法或利用兩向量叉積求解。觀察圖3.1左圖中，4個平面Pl-1~Pl-4的大圓等角度投影，Pl-1與平面Pl-2、Pl-3、 Pl-4之交線分別為i-1-2，i-1-3及i-1-4；Pl-2與平面Pl-3、Pl-4交線分別為i-2-3與i-2-4。平行於i-1-2，i-1-3，i-1-4所組成之三角形(圖3.1右圖中上部)；及由平行於i-1-2，i-2-3，i-2-4所組成之三角形(圖3.1右圖中下部)。如兩三角形中任一邊尺寸(或分量)已知，則同一三角形其餘兩邊依閉合三角形作圖法或向量運算原則可輕易解答。另相鄰之三角形，因共邊尺寸已知，亦可依序求出，此即為圖解法之原理。

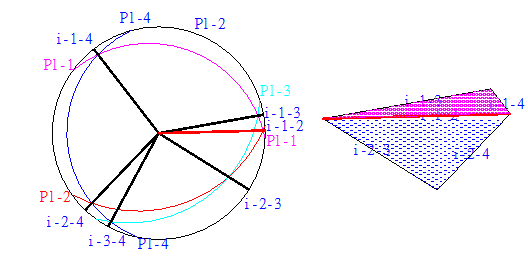
                   圖3.1岩楔等角度投影及岩楔左右滑動面三角形

3.2向量解法概述

如圖3.2(a)及3.2(b)所示岩楔，左側坡底ΔABC為平面PL-1；右側坡底ΔABD為平面PL-2；上坡面ΔACD為平面PL-3；下坡面ΔCDB為平面PL-4；圖3.2(b)中張力裂縫所在之平面ΔEFG為PL-5。PL-1與PL-2之交線為，長度為（即AB，i為單位向量，方向朝下，以下類推）；PL-1與PL-3為（長度為，即AC）；PL-2與PL-3為（長度為，即AD）；PL-1與PL-4為（長度為，即CB）；PL-2與PL-4為（長度為，即DB）；PL-3與PL-4為（長度為，即CD）；有張力裂縫時PL-1與PL-5交線為（長度為，即EF）；PL-2與PL-5為（長度為，即EG）。因為各平面之位態已知，故各交線之單位向量可依序求出。其方向假定如圖3.2(c)及圖3.2(d)所示，其中~之任一長度或x、y或z軸長度分量如果已知，則其餘可依向量加減法則，依序求出。有張力裂縫時，則、 或PL-5中任一稜線尺寸必須已知。因AB+BC+CA=0，即：

i+i+i =0

故

i+i=-i，i+i=-i
i+i=-i

如z已知，則由i．k=i=z， 故=z/ i，解聯立方程可得

=/
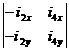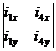
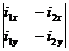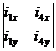=/ ................................................................. (3.1)

、求出後可依序求出、等，比照上述方式，可求出，及。（圖3.2岩楔AFEG中=AE，=AF，=AG）

A（面積） = ｜｜｜i×i｜ （取絕對值，以下同）
A=｜｜｜i×i｜
A=｜｜｜i×i｜
A =｜｜｜i×i｜
A=｜｜｜i×i｜........................................................ (3.2)

V（體積） =｜｜｜i．i×i｜
V=｜｜｜i．i×i｜........................................... (3.3)

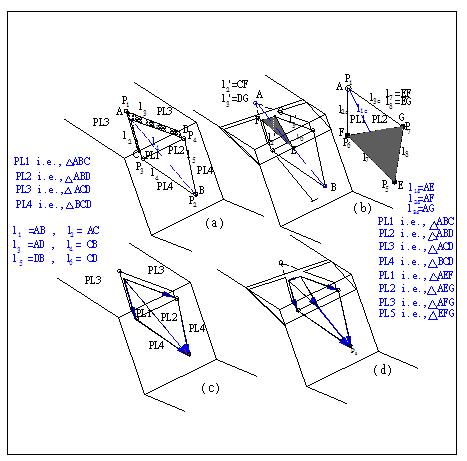
圖3.2楔形滑動不連續面關係示意圖

3.1聯立方程式解法

理論上，不共線之三點可以定義一個唯一平面，三個不平行的平面(更精確的說法是三個平面方程式非相依)可決定岩體一個頂點。如圖3.2之岩楔，因各不連續面之傾向/傾角已知，各別單位法線可以求得，d(i=1~4)亦可由邊界條件求得。因為岩楔之稜線長度、面積、體積之大小為相對關係，與座標軸選擇無關，為簡化計算工作，可假定P之座標P(x,y,z)為任意值，其中以P(0,0,0)之假設最為省事，故四個平面方程式可假設如下列：

ax+by+cz=0……………… (3.1)

ax+by+cz=0…………… (3.2)

ax+by+cz=0……………… (3.3)

ax+by+cz=d……………… (3.4)

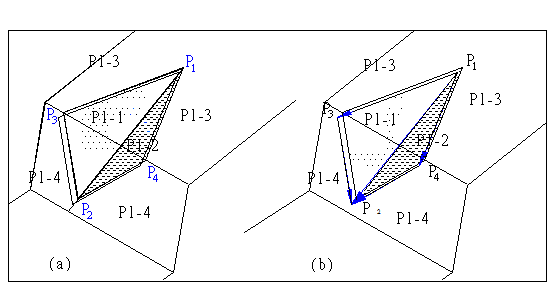
圖3.2岩楔示意圖(無張力裂縫)

解聯立方程式(3.1)、(3.2)及(3.4)可得P座標；解 (3.1)、(3.3)及(3.4)可得P座標；及解 (3.2)、(3.3)及(3.4)可得P座標。若岩楔任一稜線長度或x、y或z任一方向之長度已知時，可求出d真正大小，因而求出P~P座標值及相關各平面之面積及岩楔體積。另觀察圖3.3五個平面(含張力裂縫)的岩楔，在岩層位態及兩個稜線尺寸(至少一個在裂縫平面稜線上)，則其解法與前述方法相同。

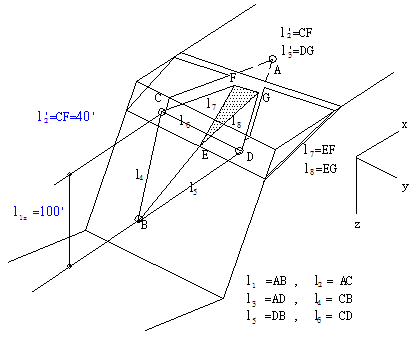
圖3.3岩楔示意圖(有張力裂縫)

3.1.1例題解答及說明

[例題E3.1]:

有一岩楔係由四個不連續面及一張力裂縫所組成(非外伸坡)：

平面(PL)   1(左側底)  2(右側底) 3(上坡)  4(下坡)   5(張力裂縫)

傾向(°)      105        235      195     185      165

傾角(°)       45         70       12      65       70

=100ft，-=40ft(圖3.3)。試求岩楔體積及兩底部接觸面面積？

[解答]:

(1)假定單位法線向量均取朝下，則各平面之單位法線向量分別為:

PL-1  105/45: [0.1830,-0.6830,0.7071]

PL-2  235/70: [0.5390,0.7698,0.3420]

  PL-3  195/12: [0.2008,0.0538,0.9781]

PL-4  185/65: [0.9029,0.0790,0.4226]

  PL-5  165/70: [0.9077,-0.2432,0.3420]

(2)代入平面方程式ax+by+cz=d公式中，可得

-0.1830x+0.6830y-0.7071z=d…………(E3.1a)

-0.5390x-0.7698y-0.3420z=d…………(E3.1b)

-0.2008x-0.0538y-0.9781z=d…………(E3.1c)

-0.9029x-0.0790y-0.4226z=d…………(E3.1d)

-0.9077x+0.2432y-0.3420=d…………(E3.1e)

(3)因點2及點3高h=100ft，故依公式()=h/︱z︱=100/0.6920=144.51(ft)，假定P(0,0,0)，解(E3.1a)、( E3.1b) 及( E3.1d)可得P；(E3.1a)、( E3.1c) 及( E3.1d)得P；解(E3.1b)、(E3.1c) 及(E3.1d)得P。計算點2~點3之距離=，由=()=144.51，求出d後，代回P、 P及 P座標，分別為P(-198.77f, 81.35, 130.00)；P(-144.085,-7.551,29.998)；P(-151.041,94.286,25,824)。

(4)點2及點6距離已知為40ft，故由點2及點6距離與比例關係可得

P(-110.370,45.193,72.219)，將P座標代入( E3.1e)可得d。解(E3.1a)、( E3.1c) 及( E4.1e)後，再將d代入得P(-104.976,-5.502,21.856)；解(E3.1b)、( E3.1c) 及( E4.1e)後，再將d代入得得P(-86.383,53.924,14.769)。

(5)A=△ABC-△AEqf=∣×∣/2-∣×∣/2=5565.01ft，

A=△ABD-△AEG=6428.13 ft，A=△EqfG=1846.54 ft，

V(岩楔)=V-V=∣．×∣/6-∣．×∣/6

=176702.25ft，

h=∣+∣/2=53.92ft，W(岩楔)=V=0.160．17602.25=28272.2kips，

即W=28272.2[0,0,1]

上述岩楔各頂點座標及各平面之面積等，可利用本人所編製的工具程式中之『多面體岩楔』求解如圖E3.1.1。

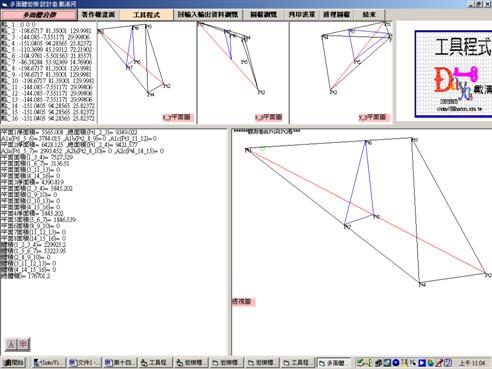
圖E3.1.1工具程式『多面體岩楔』程式求岩楔座標、面積

表4.2.1資料輸入(一)

[例題E3.]:

如下表之岩楔座標

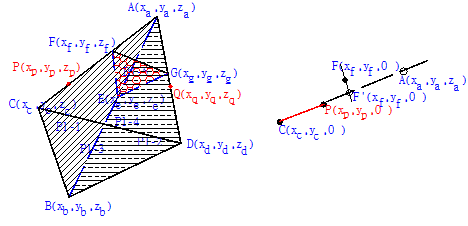
圖3.3岩楔座標試示意圖