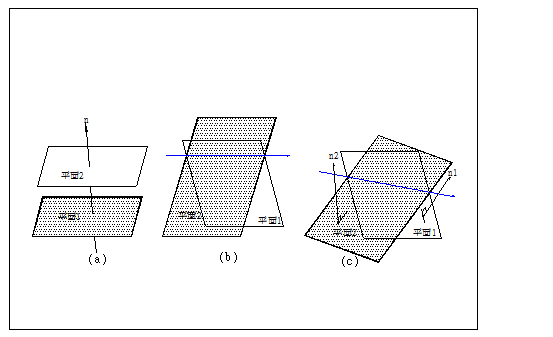
 圖1.1空間兩平面交線示意圖
圖1.1空間兩平面交線示意圖空間平面與構造平面交線
(空間平面研究系列之五)
1.前言
在岩坡穩定規劃、分析工作中,經常需處理露頭之不連續面:節理、層面與斷層相互間之交線,首先讓我們觀察圖1.1(a)兩完全平行傾角完全相等(指角度大小及傾斜方向都相同)之3D平面是永不會相交;兩傾向或傾角不相等之空間平面,必定會相交,如圖1.1(b)之兩平面走向平行但傾角不等(角度大小相同傾斜方向不同)則其交線與原走向線平行;另如圖1.1(c)中兩平面走向不平行則其交線與原走向也不平行。一般地質之位態及傾斜平面位置屬相對問題,為簡化問題如將傾斜平面假定通過地球球心,則其交線之單位向量[ux,uy,uz]之起點為地球球心(0,0,0),而終點必須是(ux,uy,uz)。岩楔滑動方向與兩平面單位交線向量平行,岩楔是否滑動?與uz大小及符號有關,如座標取x(E)、y(N)及z(Up)螺旋定則,則uz<0時岩楔可能沿單位向量[ux,uy,uz]朝下坡滑動。兩平面交線之求解與岩楔穩定分析圖解法或數學解法關係密切,因此特闢專章介紹。
 圖1.1空間兩平面交線示意圖
圖1.1空間兩平面交線示意圖
2. 兩平面之交線
首先讓我們來研究不通過地球球心之兩平面095/45及175/80,其單位朝下法線向量分別為[0.0616,0.7044,0.7071]及[0.9811,0.0858,0.1736],則兩平面方程式可假定為:
0.0616x+0.7044y+0.7071z=d![]() …………(A2.1)
…………(A2.1)
0.9811x-0.0858y+0.1736z=d![]() ……………(A2.2)
……………(A2.2)
式(A2.1)及(A2.2)中d![]() 及d
及d![]() 為任意值,若兩平面交線通過已知點(x
為任意值,若兩平面交線通過已知點(x![]() ,y
,y![]() ,z
,z![]() ),則式(A2.1)及(A2.2)可改寫為:
),則式(A2.1)及(A2.2)可改寫為:
0.0616(x
-x![]() )+0.7044(y-y
)+0.7044(y-y![]() )+0.7071(z-z
)+0.7071(z-z![]() )=0…………(A2.3)
)=0…………(A2.3)
0.9811(x
-x![]() )-0.0858(y-y
)-0.0858(y-y![]() )+0.1736(z-z
)+0.1736(z-z![]() )=0……………A2.4)
)=0……………A2.4)
將(z-z![]() )視為已知,解(x
-x
)視為已知,解(x
-x![]() )及(y-y
)及(y-y![]() )
可得x=x
)
可得x=x![]() -0.08984(z-z
-0.08984(z-z![]() ),y=y
),y=y![]() +0.9960(z-z
+0.9960(z-z![]() )
)
,如令定點x![]() =5,y
=5,y![]() =5,z
=5,z![]() =5且z-z
=5且z-z![]() =0,則z=5,x=5,y=5;如令z-
z
=0,則z=5,x=5,y=5;如令z-
z![]() =1,則z=6,x=4.9102,y=5.9960,即點(5,5,5)及(-4.9102,5.9960,6.0000)為交線上之任意兩點,故交線向量比為(-0.08984︰0.9960︰1),即向量為[-0.08984,0.9960,1.0000]=1.4142[-0.0635,0.7043,0.7071]
=1,則z=6,x=4.9102,y=5.9960,即點(5,5,5)及(-4.9102,5.9960,6.0000)為交線上之任意兩點,故交線向量比為(-0.08984︰0.9960︰1),即向量為[-0.08984,0.9960,1.0000]=1.4142[-0.0635,0.7043,0.7071]
,交線單位向量u![]() =[uix,uiy,uiz]=
[-0.0635,0.7043,0.7071]。上述單位向量之求解與(x
=[uix,uiy,uiz]=
[-0.0635,0.7043,0.7071]。上述單位向量之求解與(x![]() ,y
,y![]() ,z
,z![]() )值完全無關,因此在球體投影圖解法中可假定x
)值完全無關,因此在球體投影圖解法中可假定x![]() =0,y
=0,y![]() =0,z
=0,z![]() =0而不失其代表性。交線單位向量之求解亦可由代表兩平面之單位法線向量叉積求得(詳下節)。表2.1為解聯立方程式之Excel試算表,表2.1中之Pt1~Pt3為平面095/45上之點;Pt1’~Pt6’平面175/80上之點。圖2.1為平面095/45及175/80
x-y,y-z,x-z平面圖及3D示意圖,圖中Pt1及Pt3(或Pt1’及Pt4’)連線為兩平面之交線,x-y平面圖及3D示意圖中Pt1及Pt2連線(即PR)為平面095/45之走向,Pt1’及Pt3’連線(即PS)為平面175/80之走向。圖2.1(d)中,如將Pt2與Pt1連線(即RP),想像為觀測視線,通過Pt2之水平線(即RI),想像為觀測儀器之十字絲,Pt1與Pt3連線(即PQ),想像為峭壁露頭上不連續面之構造線,則Pt2與Pt3連線(即RQ),即為觀測儀器鏡頭上之影像(Image),Pt2與Pt3連線與通過Pt2之水平線(即RI)所成夾角,即為觀測儀器鏡頭上之視傾角。
=0而不失其代表性。交線單位向量之求解亦可由代表兩平面之單位法線向量叉積求得(詳下節)。表2.1為解聯立方程式之Excel試算表,表2.1中之Pt1~Pt3為平面095/45上之點;Pt1’~Pt6’平面175/80上之點。圖2.1為平面095/45及175/80
x-y,y-z,x-z平面圖及3D示意圖,圖中Pt1及Pt3(或Pt1’及Pt4’)連線為兩平面之交線,x-y平面圖及3D示意圖中Pt1及Pt2連線(即PR)為平面095/45之走向,Pt1’及Pt3’連線(即PS)為平面175/80之走向。圖2.1(d)中,如將Pt2與Pt1連線(即RP),想像為觀測視線,通過Pt2之水平線(即RI),想像為觀測儀器之十字絲,Pt1與Pt3連線(即PQ),想像為峭壁露頭上不連續面之構造線,則Pt2與Pt3連線(即RQ),即為觀測儀器鏡頭上之影像(Image),Pt2與Pt3連線與通過Pt2之水平線(即RI)所成夾角,即為觀測儀器鏡頭上之視傾角。
如某構造面上之構造線PQ位態未知,但現場觀測視線向量位態及視傾角(或側傾角)已知時,由視傾角(或側傾角)定義可求出構造線影像向量RQ,而平面PQR可以RP與RQ兩向量之叉積定義, PQ位態為平面PQR及平面PQS之公交線。
表2.1聯立方程式求兩平面交線Excel試算表
|
plane |
?did(deg) |
?dip(deg) |
a |
b |
c |
detx |
dety |
detz |
ll |
|
|
1 |
95 |
45 |
0.0616 |
-0.7044 |
0.7071 |
-0.0616 |
0.6830 |
0.6858 |
0.9698 |
|
|
2 |
175 |
80 |
0.9811 |
-0.0858 |
0.1736 |
|
|
|
|
|
|
|
ux |
uy |
uz |
did(deg) |
did(deg) |
dip(deg) |
|
|
|
|
|
|
-0.0635 |
0.7042 |
0.7071 |
95.16 |
95.16 |
45.00 |
|
|
|
|
|
|
-0.0635 |
0.7042 |
0.7071 |
|
|
|
|
|
|
|
|
plan1 |
x |
y |
z |
d |
l12? |
plan2 |
x |
y |
z |
d |
|
pt1 |
5.0000 |
5.0000 |
5.0000 |
0.3216 |
4.0000 |
pt1’ |
5.0000 |
5.0000 |
5.0000 |
5.3444 |
|
pt2 |
4.0000 |
4.9125 |
5.0000 |
0.3216 |
|
pt2’ |
5.0000 |
7.0231 |
6.0000 |
5.3444 |
|
pt3 |
4.7458 |
7.8170 |
7.8284 |
0.3216 |
|
pt3’ |
5.1390 |
6.5889 |
5.0000 |
5.3444 |
|
|
|
|
|
|
|
pt4’ |
4.7458 |
7.8170 |
7.8284 |
5.3444 |
|
plane1 |
x |
y |
z |
vx |
vy |
vz |
detx |
dety |
detz |
ll |
|
pt1 |
5.0000 |
5.0000 |
5.0000 |
-1.0000 |
-0.0875 |
0.0000 |
-0.2475 |
2.8284 |
-2.8392 |
4.0153 |
|
pt2 |
4.0000 |
4.9125 |
5.0000 |
-0.2542 |
2.8170 |
2.8284 |
|
|
|
|
|
pt3 |
4.7458 |
7.8170 |
7.8284 |
|
|
|
|
|
|
|
|
|
a |
b |
c |
did(deg) |
did(deg) |
dip(deg) |
|
|
|
|
|
|
-0.0616 |
0.7044 |
-0.7071 |
95.0000 |
95.00 |
45.00 |
|
|
|
|
|
plane2 |
x |
y |
z |
vx |
vy |
vz |
detx |
dety |
detz |
ll |
|
pt1 |
5.0000 |
5.0000 |
5.0000 |
0.0000 |
2.0231 |
1.0000 |
2.9053 |
-0.2542 |
0.5142 |
2.9614 |
|
pt2 |
5.0000 |
7.0231 |
6.0000 |
-0.2542 |
2.8170 |
2.8284 |
|
|
|
|
|
pt3 |
4.7458 |
7.8170 |
7.8284 |
|
|
|
|
|
|
|
|
|
a |
b |
c |
did(deg) |
did(deg) |
dip(deg) |
|
|
|
|
|
|
0.9811 |
-0.0858 |
0.1736 |
175.0000 |
175.00 |
80.00 |
|
|
|
|
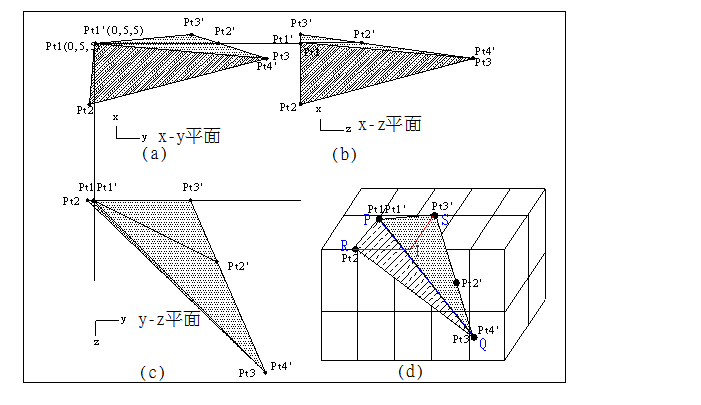 圖2.1平面095/45及175/80
x-y,y-z,x-z平面圖及3D示意圖
圖2.1平面095/45及175/80
x-y,y-z,x-z平面圖及3D示意圖
2.2等角度大圓投影圖解法
兩平面交線球體投影圖解法,不論是等角度或等面積投影,均為投影基圓圓心與兩平面投影曲線交點之連線。
[例題E2.2]:
試繪製平面160/35與210/30之交線等角度投影圖?
[解答]:
(a)投影網圖解法
(1)先在透明紙上畫基圓及圓心(0,0)後標示NS軸,依一般平面描繪160/35之投影大圓及極點如圖E2.2.1a。
(2)依同樣程序描繪210/30之投影大圓及極點如圖E2.2.1a。
(3)連接圓心與大圓A、B兩弧交點間直線並標示為ab如圖E2.2.1b。
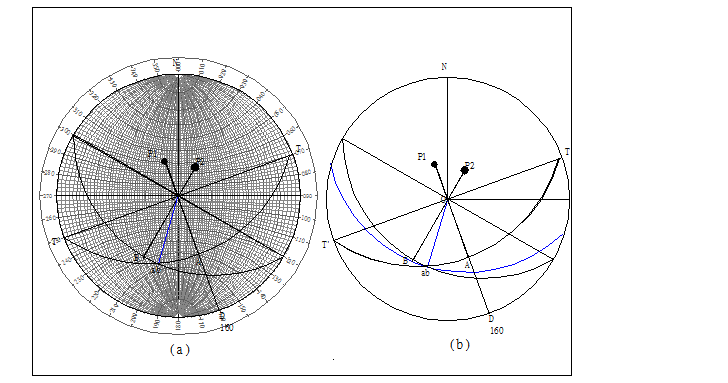 圖E2.2.1平面160/35及210/30交線等角度投影圖
圖E2.2.1平面160/35及210/30交線等角度投影圖
(b)不用投影網之圖解法
(1)選擇適當位置為中心,以任意長度(ρ=1單位長度)為半徑,通過圓心畫相互垂直之兩直徑,直徑最上端標示北方(N)右端標示東方(E)。通過圓心量一角度(由北起算)等於傾向160°畫半徑OM(傾向之投影方向),畫與傾向垂直之直徑TT’(平面走向之投影位置)。
(2)沿傾向之投影方向(由圓心起算)量取距離OA=ρtan(45°-β/2)
=tan(27.5°)=0.5206單位長度,OA代表通過地球中心之平面沿重力滑動方向(傾向)朝下單位向量在下半球之投影,如為朝上單位向量則改為上半球投影,其投影為OA’(OA’距離等於OA但方向相反,即OA’為OA之反向量)。
(3)過T、A、T’三點畫圓弧,或以(-cos160°tan35°,-sin160°tan35°),即(0.6580,-0.2395)為圓心,半徑為1/cos35°=1.22單位長度畫圓弧。圓弧TAT’即代表通過地球中心之平面(即ax+by+cy=d=0,[a,b,c]為平面單位法線)在水平面投影大圓A。
(4)沿OA反向量取OP1=tan(β/2)=0.3153單位長度,點P1即160/35之極點投影(圖E2.2.2)。
(5)平面B之作法同平面A。
(6)連接圓心與大圓A、B兩弧交點間直線並標示為ab。
(7)交線ab之傾向為Atan2(-0.1677,-0.5607)=196.65°,由
cos(196.65)tan(45-β/2)=-0.5607,可得β=29.33°。
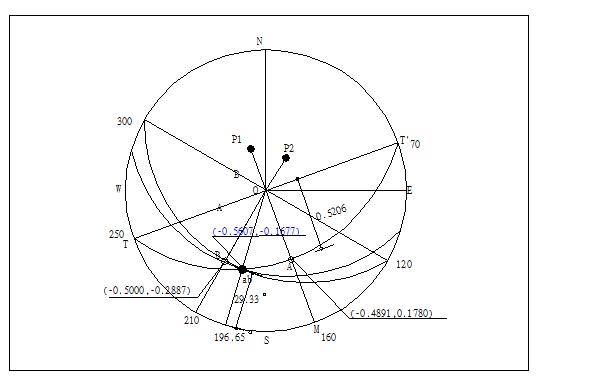 圖E2.2.2平面160/35及210/30交線等角度投影圖
圖E2.2.2平面160/35及210/30交線等角度投影圖
2.3 向量叉積解法
(1)平面160/35及210/30之朝下單位法線向量分別為[nx1,ny1,nz1]=[0.5390,-0.1962,0.8192],
[nx2,ny2,nz2]=[0.4330,0.2500,0.8660],交線向量U![]()
U![]() =
=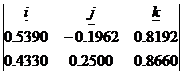 =
= ![]() i
-
i
- ![]() j
+
j
+![]() k=[-0.3747,-0.1121,0.2197]
k=[-0.3747,-0.1121,0.2197]
=0.4486[-0.8353,-0.2498,0.4989]
did=Atan2(-0.2498,0.8353)=196.65°
dip=Asin(0.4898)=29.33°
在此要特別提醒讀者,兩向量叉積為位置向量非法線向量,故由向量求傾向時不必加180°,傾角為Asin()非Acos()。
(2)表E2.2.3為利用兩平面法線向量叉積公式求交線之Excel試算表,表中
xprj(n),yprj(n)為平面之朝下單位法線向量等角度投影位置,xprj,yprj為交線單位向量等角度投影位置。xicen,yicen及ricen分別為以交線單位向量之平面等角度投影大圓心x、y座標及半徑。
表E2.2.3利用兩平面法線向量叉積公式求交線Excel試算表
|
plane |
? bear. |
?pitch |
nx(I) |
ny(I) |
nz(I) |
xprj(n) |
yprj(n) |
|
|
1 |
160.00 |
35.00 |
0.5390 |
-0.1962 |
0.8192 |
0.2963 |
-0.1197 |
|
|
2 |
210.00 |
30.00 |
0.4330 |
0.2500 |
0.8660 |
0.2321 |
0.1443 |
|
|
plane |
x |
y |
z |
xprj |
yprj |
xcen |
ycen |
r |
|
1 |
-0.7698 |
0.2802 |
0.5736 |
-0.4892 |
0.1780 |
0.6580 |
-0.2395 |
1.2208 |
|
2 |
-0.7500 |
-0.4330 |
0.5000 |
-0.5000 |
-0.2887 |
0.5000 |
0.2887 |
1.1547 |
|
2 vector |
cross |
prodoct |
|
|
|
|
|
|
|
|
nx(I) |
ny(I) |
nz(I) |
UIX |
UIY |
UIZ |
LUI |
|
|
vect.1 |
0.5390 |
-0.1962 |
0.8192 |
-0.3747 |
-0.1121 |
0.2197 |
0.4486 |
|
|
vect.2 |
0.4330 |
0.2500 |
0.8660 |
|
|
|
|
|
|
unit |
vector |
of |
intesec. |
line |
|
|
|
|
|
uix |
uiy |
uiz |
didi |
dipi |
didf(deg) |
dipf(deg) |
xprj |
yprj |
|
-0.8353 |
-0.2498 |
0.4898 |
-163.35 |
29.33 |
196.65 |
29.33 |
-0.5607 |
-0.1677 |
|
na |
nb |
nc |
xicen |
yicen |
ricen |
|
|
|
|
0.4692 |
0.1403 |
0.8719 |
0.5382 |
0.1610 |
1.1470 |
|
|
|
2.4 聯立方程式解法
(1)平面160/35及210/30之朝下單位法線向量分別為[nx1,ny1,nz1]=[0.5390,-0.1962,0.8192],
[nx2,ny2,nz2]=[0.4330,0.2500,0.8660],故其對應之方程式可假定如
0.5390x-0.1962y+0.8192z=d1
0.4330x+0.2500y+0.8660z=d2
(2)平面交線方向與d1及d2值無關,故可假定交線通過(0,0,0),即d1=d2=0
如z=1,上兩式可改為
0.5390x-0.1962y=-0.8192
0.4330x+0.2500y=-0.8660
解方程式得x=1.7055,y=-0.5102
(3)交線向量為[1.7055,0.5102,1]=2.0418[0.8353,-0.2498,0.4898]
did=Atan2(-0.2498,0.8353)=196.65°,dip=Asin(0.4898)=29.33°
(4)圖E2.2.3為利用電腦程式計算結果及圖示。
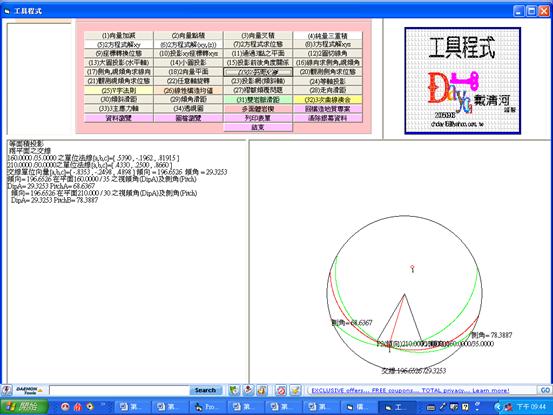
圖E2.2.3電腦程式計算結果及圖示