空間平面方程式與等角度投影
(空間平面系列之三)
1.前言
傳統之等角度或等面積投影,需利用已繪製完成之投影網圖,繪圖作業及資料處理不甚方便,尤其是在處理平面繞傾斜軸旋轉投影作業時,既費時費力,也容易出錯。為配合P.C電腦作業,因此筆者早在1987(現代營建88~90期)曾推導出等角度及等面積投影之基本公式,為讀者提供一套既完整又清晰之觀念,並能對圖解法答案之校核或對岩坡穩定問題及構造地質學之研究,有所助益。所謂等角度投影(Equal angle projection)亦稱立體投影(Stereographic projection),或稱伍爾夫投影(Wulff projection);至於等面積投影(Equal area projection),亦稱之為施密特法(Schimidt method)。
2.等角度投影
今如假定通過參考球體中心之赤道面圖2.1)為投影水平面,則投影水平面與參考球體相交之軌跡稱之為投影基圓(Primitive
circle)。根據定義:等角度投影為代表空間向量之A點(圖2.1)及天頂(Zenith)T點[單位球體座標(0,0-1)]連線,與通過參考球體球心之水平面(基圓)相交於A![]() 點,此A
點,此A![]() 點即為A點之等角度投影點。若將參考球體上大圓圓周每一個點與球體天頂T連接,則各連接線圍成一圓錐體(基圓通過球心),此圓錐體與投影水平面相交之處為圓。如僅考慮下半球之投影,則參考球體大圓與投影平面相交部分為圓弧,此圓弧即為下半球球體投影之全景軌跡投影(Cyclographic
projection)。今假定取通過球心O(0,0,0),並包含圖2.1中任意向量OA之垂直平面如圖2.2所示者,因任意向量OA之傾向為p,傾角為q,OP為垂直不連續面之單位法線向量,則依等角投影之定義,A
點即為A點之等角度投影點。若將參考球體上大圓圓周每一個點與球體天頂T連接,則各連接線圍成一圓錐體(基圓通過球心),此圓錐體與投影水平面相交之處為圓。如僅考慮下半球之投影,則參考球體大圓與投影平面相交部分為圓弧,此圓弧即為下半球球體投影之全景軌跡投影(Cyclographic
projection)。今假定取通過球心O(0,0,0),並包含圖2.1中任意向量OA之垂直平面如圖2.2所示者,因任意向量OA之傾向為p,傾角為q,OP為垂直不連續面之單位法線向量,則依等角投影之定義,A![]() ,P
,P![]() 分別代表向量OA及
OP水平面之投影位置。如令OA=〔x
分別代表向量OA及
OP水平面之投影位置。如令OA=〔x![]() ,y
,y![]() ,z
,z![]() 〕=[cos(p)cos(q),sin(p)cos(q),sin(q)]…………………(2.1)
〕=[cos(p)cos(q),sin(p)cos(q),sin(q)]…………………(2.1)
又令參考球體半徑為1單位長度,則
|OA![]() |=tan(45°-
|=tan(45°-![]() )………………(2.2)
)………………(2.2)
假設A(x![]() ,y
,y![]() ,z
,z![]() )點在投影水平面之投影點A
)點在投影水平面之投影點A![]() 之座標為(x,y,0),則
之座標為(x,y,0),則
x²+y²=tan²(45°- ![]() )=
)=![]() ……………………………………(2.2)
……………………………………(2.2)
因T(0,0,-1)、A、A![]() 三點共線,可求得:
三點共線,可求得:
故x=±![]() (下半球投影,z>0 取正號,z<0
取負號)…… (2.3a)
(下半球投影,z>0 取正號,z<0
取負號)…… (2.3a)
x=cos(p)tan(pi/4-q/2) …… (2.3b)
y=±![]() (z>0 取正號,z<0
取負號……(2.3c)
(z>0 取正號,z<0
取負號……(2.3c)
y=sin(p)tan(pi/4-q/2) …… (2.3d)
式(2.3)為空間任意點A(x![]() ,y
,y![]() ,z
,z![]() )等角度投影至赤道平面上點A
)等角度投影至赤道平面上點A![]() (x,y,0)基本之轉換公式,如為上半球投影,則依式(3.4)所計算出之x,y必須變號。公式2.3為可逆性(Reversible)公式,由投影座標x,y則可反算x
(x,y,0)基本之轉換公式,如為上半球投影,則依式(3.4)所計算出之x,y必須變號。公式2.3為可逆性(Reversible)公式,由投影座標x,y則可反算x![]() ,y
,y![]() ,z
,z![]() 。
。
x![]() =2x/(1+x
=2x/(1+x![]() +y
+y![]() )……(2.3e)
)……(2.3e)
y![]() =2x/(1+x
=2x/(1+x![]() +y
+y![]() )……(2.3f)
)……(2.3f)
z![]() =(1-x
=(1-x![]() -y
-y![]() )/(1+x
)/(1+x![]() +y
+y![]() )……(2.3g)
)……(2.3g)
圖2.3為利用式(2.3)所求出之投影後大圓圓心、極點及傾向位置點之綜合示意圖。
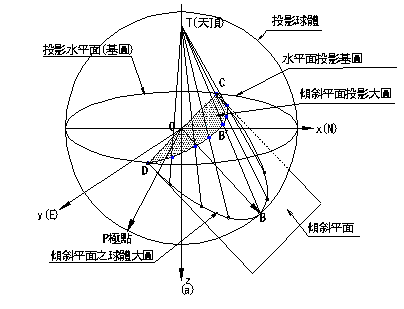
圖2.1平面等角度投影關係示意圖
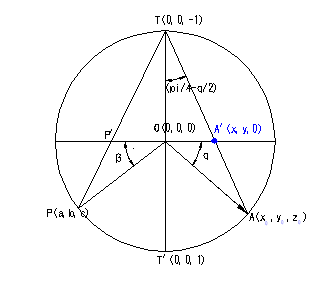
圖2.2任意向量等角度投影示意圖
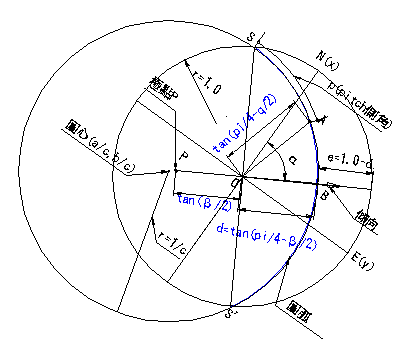
圖2.3等角度圓心、極點及傾向投影示意圖
空間平面上單位球體上大圓之任意座標(x,y,z)可利用公式(2.3)將其一一投影至水平面上,連接所有之投影點即為所求之等角度投影投影大圓,或利用公式(2.4)直接繪製。
(x-![]() )
)![]() +(y-
+(y-![]() )
)![]() =
=![]() ……………………………(2.4)
……………………………(2.4)
上式中[a,b,c]為通過球心之平面ax+by+cz=0之單位朝下法線向量。
另觀察如圖2.4中,假設不通過圓心之任意平面ABC與單位球體所截之圓上任意單位位置向量d,e為垂直於平面ABC之單位向量,
e
=〔e![]() ,e
,e![]() ,e
,e![]() 〕……………………………(2.5)
〕……………………………(2.5)
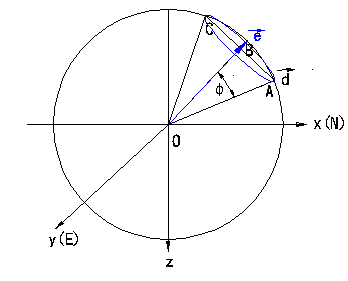
圖2.4不過圓心平面(小圓)投影關係示意圖
d
=〔d![]() ,d
,d![]() ,d
,d![]() 〕=〔cospcosq,sinpcosp,sinq〕…………(2.6)
〕=〔cospcosq,sinpcosp,sinq〕…………(2.6)
如d繞e旋轉,由e.d=cos![]() 關係可得:
關係可得:
(x-![]() )
)![]() +(y-
+(y-![]() )
)![]() =(
=(![]() )
)![]() ………(2.7)
………(2.7)
式(2.7)中如![]() =90°,則e=[a,b,c],則式(2.7)同式(2.4),此即表示大圓等角度投影為小圓等角度投影之特例。
=90°,則e=[a,b,c],則式(2.7)同式(2.4),此即表示大圓等角度投影為小圓等角度投影之特例。
3.等角度投影網電繪製原理介紹
不論是單位向量或大小圓等角度投影圖繪製,都可利用投影基本公式直接作業。唯如等角度投影圖網,或等面大小圓投影圖及投影圖網繪製,或構造地質學、岩坡工程學向量(平面)旋轉等之圖解法作業中,在過去電腦並不普遍之年代,是相當費時費力且容易出錯,精確度亦不高。此類投影圖之電腦繪製工作,過去都是非常專業的,也非常神秘,尤其是繞傾斜軸旋轉者,更是珍貴的不得了(好像是屬專賣?)。但所謂『江湖一點訣,說破不值一文錢』,讓筆者說給您知道,其實只要利用平面方程式再加上一點小技巧,您也可以自己動手D.I.Y一番。如圖3.1中之任意平面(小圓)方程式為:ax+by+cz=d,(![]() =1.0,
=1.0,![]() =1.0),與大圓(方程式ax+by+cz=0)。今如欲繪製小圓之圖像及其對應之等角度(或等面積)小圓之投影網圖時。因任意平面單位法線向量=
[a,b,c]為已知,平面上任意向量為
=1.0),與大圓(方程式ax+by+cz=0)。今如欲繪製小圓之圖像及其對應之等角度(或等面積)小圓之投影網圖時。因任意平面單位法線向量=
[a,b,c]為已知,平面上任意向量為
[x,y,z]=[cos(p)cos(q),sin(p)cos(q),sin(q)] …………………(3.1)
,因[a,b,c]•[x,y,z]=cos(θ),可得: acos(p)cos(q)+bsin(p)cos(q)+csin(q)=cos(θ)=d…………………(3.2)
公式(3.2)中cos(θ)已知,如令l=acos(q),m=bcos(q),n=cos
(θ)-csin(q) ,利用三角函數公式:![]() =
=![]() ,假定q=t°,可求出對應之p值。
,假定q=t°,可求出對應之p值。
代入公式(4.2)可求出[x,y,z],然後假定q=2t°,q=3t°,…………………,可求出各對應之[x,y,z]。將所有之[x,y,z]代入等角度[公式(2.3)*]中,可得對應之投影點(x![]() ,
y
,
y![]() ),即
),即
x![]() =±
=±![]() ,y
,y![]() =±
=±![]() (z>0取正號,z>0取負號)
,
(z>0取正號,z>0取負號)
,
以圓滑曲線連接各投影點後,對應之圖示即為所求。
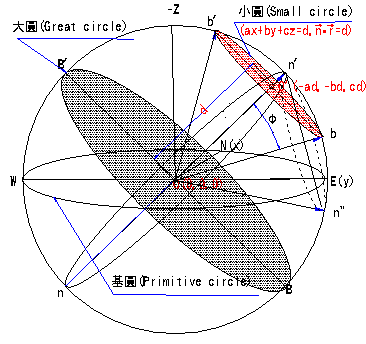
圖3.1任意平面與單位球體相交圖形示意圖
上述求解亦可改先假定p然後求q,其餘步驟與假定q後求p相似。
前面兩種求(p,q)、[x,y,z]及(x![]() ,
y
,
y![]() )方法在平面接近鉛垂時(即法線接近水平),會發生(p,q)解答困難或誤差甚大之情形。為解決前述缺憾,首先求出一個(p,q)及對應之[x,y,z]值後,利用向量繞任意軸旋轉公式,將向量Op繞OT旋轉
)方法在平面接近鉛垂時(即法線接近水平),會發生(p,q)解答困難或誤差甚大之情形。為解決前述缺憾,首先求出一個(p,q)及對應之[x,y,z]值後,利用向量繞任意軸旋轉公式,將向量Op繞OT旋轉![]() (5°或10°),求其旋轉後之[x
(5°或10°),求其旋轉後之[x![]() ,y
,y![]() ,z
,z![]() ]及(x
]及(x![]() ,
y
,
y![]() ),依相同程序旋轉2
),依相同程序旋轉2![]() ,3
,3![]() ,…………,n
,…………,n![]() =360°。連接所有之(x
=360°。連接所有之(x![]() ,
y
,
y![]() )即為所求之小圓投影。
)即為所求之小圓投影。
Oq=[x![]() ,y
,y![]() ,z
,z![]() ]=(
Op•r)(1-cos
]=(
Op•r)(1-cos![]() )r+cos
)r+cos![]() (
Op )+sin
(
Op )+sin![]() (
Op×r)………(3.3)
(
Op×r)………(3.3)
至於包含Op及TT’之大圓平面OTpT’,亦可以比照小圓投影方式,以Op為起點旋轉一周,求對應之[x![]() ,y
,y![]() ,z
,z![]() ]及(x
]及(x![]() ,
y
,
y![]() ),連接所有之(x
),連接所有之(x![]() ,
y
,
y![]() )即為所求之大圓投影。解合乎ax+by+cz=d,
)即為所求之大圓投影。解合乎ax+by+cz=d,![]() =1.0,
=1.0,![]() =1.0三方程式之任意點座標(x,y,z)VB電腦程式,您可上網站http://www.chday169.url.tw下載Sub
OnePointOnUnitsphere)或Sub PointOnUnitsphereGiven1Variable()。
=1.0三方程式之任意點座標(x,y,z)VB電腦程式,您可上網站http://www.chday169.url.tw下載Sub
OnePointOnUnitsphere)或Sub PointOnUnitsphereGiven1Variable()。
圖3.2及圖3.3分別為2x+4y+2z=0平面小圓及2x+4y+2z=5平面大圓的全軌跡投影(紅色線條,藍色為基圓)。
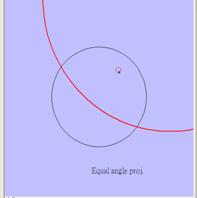
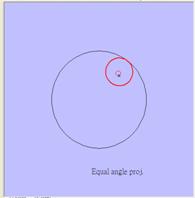
圖3.2等角度投影((2x+4y+2z=0) 圖3.3等角度投影((2x+4y+2z=5)
圖3.4即為利用前述方法利用電腦所繪製之等角度投影網(旋轉軸090/0.01),圖3.5為旋轉軸080/30等角度投影網,表3.1為利用Excel VBA為130/60,ψ=90的平面大圓等角度投影(全軌跡下半球投影),表3.2為130/60,ψ=50的平面小圓等角度投影(全軌跡下半球投影)。
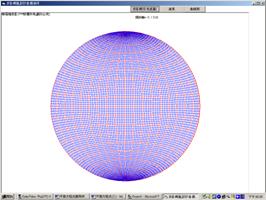
 圖3.4電腦繪製之等角度投影網(旋轉軸000/0.01)
圖3.5電腦繪製之等角度投影網(旋轉軸080/30)
圖3.4電腦繪製之等角度投影網(旋轉軸000/0.01)
圖3.5電腦繪製之等角度投影網(旋轉軸080/30)
表3.1 130/60ψ=90平面大圓等面積投影Excel試算表
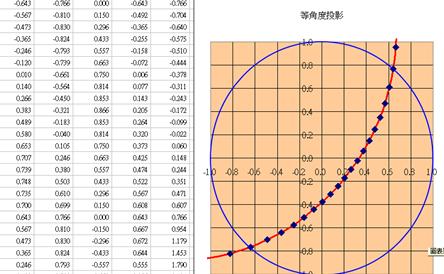
表3.2 130/60ψ=50平面小圓等角度投影Excel試算表
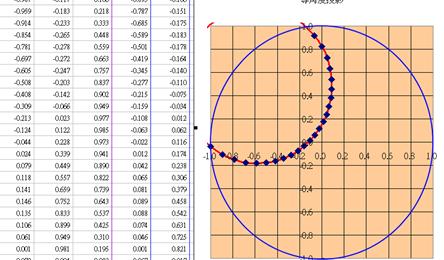
如圖3.5為130/30大圓投影圖,有關其與走向N40側傾角、視傾角的量測,除可以圖中座標,依公式計算外,如依投影網,側傾角則沿基圓圓周(360°係均勻分佈)量測,視傾角則以投影網縱橫軸為為尺規,量測時將大圓走向與南北軸重疊(詳圖3.6),然後量測東西軸大圓傾向與投影網圓周間角度。
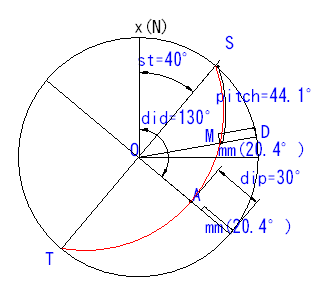
圖3.5 130/30大圓投影與走向N40視傾角、側傾角關係圖
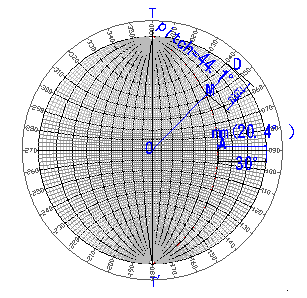
圖3.6 130/30大圓投影與走向N40視傾角、側傾角量測
4.等角度性質
依據等角度投影之原理,空間任意兩平面(向量),投影後該兩平面之夾角(方向)保持相等(此特性在向量解法或圖解法求岩楔頂點座標時非常重要),而參考球體上之面積經投影後形狀雖無改變,但面積則有所改變。等角度投影之大圓、小圓及摩擦錐等投影都屬圓曲線,因此製圖簡單又方便。表4.1為兩平面3D夾角與等角度、等面積投影後夾角變化。圖4.1為等角度投影後投影曲線間夾角變化;圖4.2為圓錐角20°時摩擦錐之等角度投影變化。綜合前述討論後,可將等面積投影與等角度投影性質綜合歸納如表4.2所示,表4.2中α、β代表向量之傾向與正傾角,任意向量之傾向及傾角則另以p、q代表。空間座標(X,Y,Z)經投影後之平面座標則以(x、y)表示,基圓之半徑均假定為1個單位長度。
表4.1 空間3D及2D夾角變化
|
平面1 |
平面2 |
3D夾角(°) |
投影等角度圖解夾角(°) |
|
354/50 |
288/41 |
46.41 |
46.45 |
|
354/50 |
316/65 |
35.04 |
35.06 |
|
354/50 |
090/34 |
60.78 |
60.89 |
|
288/41 |
316/65 |
32.44 |
32.52 |
|
288/41 |
090/34 |
73.93 |
73.96 |
|
316/65 |
090/34 |
90.10 |
89.89 |
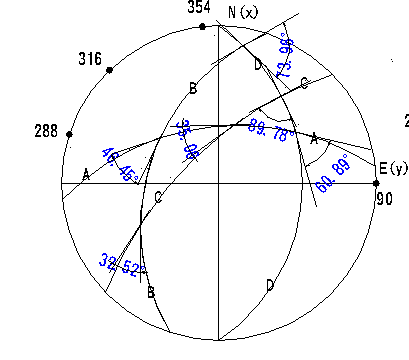
圖5.1等角度投影平面夾角
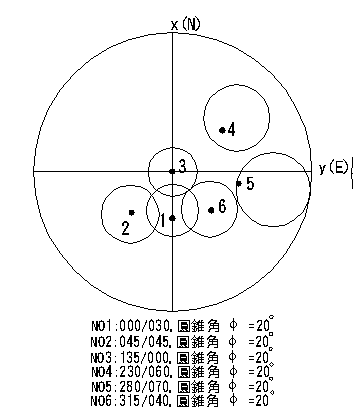
圖4.2等角度投影小圓面積變化
表4.2 等角度投影性質綜合表
|
項次 |
等角度投影 |
|
|
1 |
投影性質不變者 |
角度 |
|
2 |
投影性質改變者 |
面積 |
|
3 |
投影後圖形 |
圓 |
|
4 |
向量(線)投影圖形 |
點 |
|
5 |
球體大圓投影後 |
|
|
6 |
球體小圓投影後 |
圓 |
|
7 |
控制方程式 |
x
=±X/(1+ |
|
8 |
投影座標原點至 傾向投影點距離 |
tan(45°- |
|
9 |
走向投影座標至 極點投影點距離 |
tan( |
|
10 |
走向投影後 |
x =cos( |
|
11 |
傾向投影後 |
x=cos(α)tan(45°- |
|
12 |
極點投影後座標(下半球) |
x=-cos(α)tan( |
|
13 |
任意向量p/q投影點座標 |
x=cos(p)tan(45°- |
|
14 |
投影後曲線 |
(x- |
|
15 |
小圓投影曲線 |
[x- |
|
16 |
大圓投影求兩向量3D夾角 |
cos( |
|
17 |
等角度小圓投影求兩向量3D夾角 |
sin( |
*
t![]() =1+x
=1+x![]() +y
+y![]() ;t
;t![]() =1+x
=1+x![]() +y
+y![]() ,θ為圓錐角之半
,θ為圓錐角之半
如3D向量座標為[(x![]() ,y
,y![]() ,z
,z![]() ),i=1,2],其對應之投影座標為(x
),i=1,2],其對應之投影座標為(x![]() ,y
,y![]() ,0),
,0),
則空間中之任意兩個向量之夾角![]() 與等角度投影(或等面積2D)圖上之圓心角
與等角度投影(或等面積2D)圖上之圓心角![]() 間之關係,表4.2中角度關係可以下列方程式表示:
間之關係,表4.2中角度關係可以下列方程式表示:
cos![]() =A
=A![]() A
A![]() cos
cos![]() +B
+B![]() B
B![]()
A![]() =
=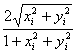
B![]() =
=![]() =
z
=
z![]() (i=1~2)
(i=1~2)