，θ有人稱之為岩樣層角(Core-bedding
angle))。該段岩樣，經取出後原來之正確走向必定改變。但不管如何改變OV與ON之夾角，並不會隨岩樣旋轉而改變，如ON長度固定，ON繞OV旋轉時ON所畫過之軌跡為一圓錐體，此圓錐體端部平面必平行岩樣斜面。假定鑽孔孔位之單位位置向量為r=[x
,y,z]，岩樣平面之單位法線向量為n=[a,b,c]，則n．r=±cosθ空間平面與鑽探取樣求岩層位態
(空間平面研究系列之七)
一、前言
利用岩層鑽探取樣的地質調查作業，為研究岩層結構之重要方式之一，尤其是在大地工程或應用地質學方面佔極重要之地位。過去鑽探取樣推求岩層位態多採用等角度投影或正交投影繪圖方式，工作繁瑣並容易出錯。而大部份之教科書只強調作業程序而忽略原理，對初學者來說，似乎有些艱澀？有鑑於此，本文特別提出數學解法及若干例題詳細說明及闡釋。
二、鑽探取樣求構造面位態
從鑽探過程中，回水量多寡及顏色、取得岩樣顏色、品質變化、岩樣斜面長軸與其中心線之夾角及夾層間填充物等，可提供很多有用資料，供地質師及工程師做為岩層分類、強度、位態推算參考或比對之用。
一般鑽探孔孔口中心或不連續面岩樣取樣之位置座標多為已知，而鑽探取得之岩樣，除非利用特殊之定向岩心取樣器或特殊攝影機器，否則由於取樣時旋轉，岩心不連續面走向無法直接藉岩樣位態判定。但岩樣不連續面之中心線與岩心平面之垂直法線交角可藉量角器量得或公式計算求得，其值不會因位置而改變。今考慮如圖2.1所示之鑽孔中某一深度一段岩樣，假設其中心軸線為OV，通過斜面中心O且在平面上之任意直線OP,
平面法線ON，並假定OH垂直於OV。如∠VON=∠HOP=θ(tanθ=，θ有人稱之為岩樣層角(Core-bedding
angle))。該段岩樣，經取出後原來之正確走向必定改變。但不管如何改變OV與ON之夾角，並不會隨岩樣旋轉而改變，如ON長度固定，ON繞OV旋轉時ON所畫過之軌跡為一圓錐體，此圓錐體端部平面必平行岩樣斜面。假定鑽孔孔位之單位位置向量為r=[x,y,z]，岩樣平面之單位法線向量為n=[a,b,c]，則n．r=±cosθ
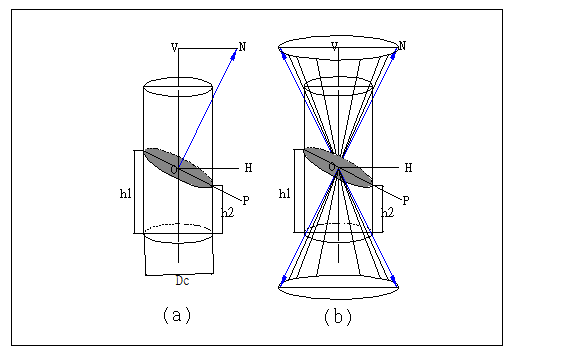圖2.1岩樣角度旋轉示意圖
i.e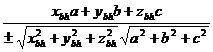 
=cosθ……………(2.1)
如岩樣破碎致傾角無法量測，但判定為同一層的岩樣，則鑽探岩樣或位置座標r=[x
,y,z]已知後，亦可利用平面空間向量或平面方程式求取不連續面位態。式(2.1)中之
，如r為單位位置向量時，則=1；而[a,b,c]為未位數，解聯立方程式時，如
≠1時，因為非線性方程組，故求解不易。因此求解時可先假設=1.0，如最後所求答案代入原方程式吻合，且≒1.0時，則所求答案方始正確。公式(2.1)中如=1及 =1時，與向量[a,b,c]繞任意軸
[x,y,z]旋轉之公式相當。
觀察圖2.2鑽孔單位向量繞岩樣單位法線旋轉示意圖中，互不平行亦不在同一直線上三個鑽探孔，鑽探單位位置向量繞岩層單位法線向量所圍成之雙圓錐面均互相平行。易言之，如三個鑽探岩樣斜面法線如果相互平行，則三個鑽探岩樣斜面必須互相平行。
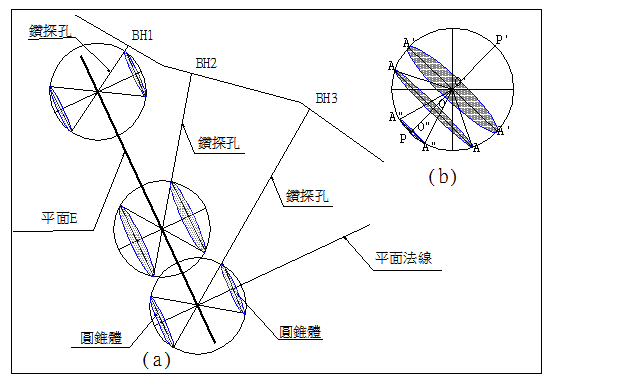圖2.2鑽孔位置向量繞岩樣法線旋轉示意圖
2.2鑽探位態數學解法
ax+by+cz=d類型之平面方程式，如其有唯一解，則其必須有三個獨立之條件方程式。一般而言，一個鑽探孔可提供至少一個條件方程式。如果鑽孔安排妥當確實，兩個傾斜鑽探孔有時亦可求得岩層之真正位態。理論上，由兩鑽探孔之岩層取樣深度之條件方程式，消去d後可得一條件方程式，由兩鑽探孔口之方位、傾角、岩樣節理資料等可求得另外兩個條件方程式，三個條件有可能解出唯一之[a,b,c]。
2.2.1三個鑽探孔
三個鑽探孔所建立之條件方程式如果不是相依(三個方程式未知數係數之行
列數Determine值不等0者)時，則三個方程式有唯一解。此與前空間平面研究系列之二的三點問題類似，不同是資料之取得，一個是由地質圖量測，一個由鑽探取得。三個取自不同鑽探孔某特定位置岩樣，如屬同一個構造面者，則取樣點之實際位置必在該構造平面上，利用三點可組成兩個向量，由兩向量之叉積，或利用三點共面之特性求取位態。如取樣深度未曾丈量，僅鑽探孔線向/傾沒角及岩心層角已知時，三個鑽探孔不一定有唯一解，其解法可先假定=1.0，然後解3個聯立方程式，或消除3個方程式等號右端常數項後，得2個方程式。如3個鑽鑽探孔有部份鑽探孔線向/傾沒角及岩心層角已知，也有部份岩樣取樣位置已知者，則宜先由性質相同之方程式消除等號右端常數項後，再與未消除常數項之方程式聯立求解。
[例題2.1]:
有三個斜向鑽孔，BH-1鑽孔方位為235/25；BH-2鑽孔方位為150/40；BH-3鑽孔方位為050/24，各孔之岩層平面與岩樣中心之夾角，分別為48°，20°，及60°，試求該岩層之位態(題目取材自Phillps 1971)?
[解:答]:
(1)如先令=1.0，
因為岩樣斜面長軸與其中心之夾角為48°，即岩樣斜面之法線與其中心之夾角為42°，故
-0.5198a-0.7424b+0.4226c=±0.7431…………(E7.1a)
(2)由BH-2斜向鑽孔之單位位置向量[x
,y,z]及岩樣斜面長軸與其中心之夾角為20°，可得
-0.6634a+0.3830b+0.6428c=±0.3420…………(E7.1b)
(3)由BH-3斜向鑽孔之單位位置向量及岩樣斜面長軸與其中心之夾角為60°，可得： 5872a+0.6998b+ 0.4067c=±0.8660…………(E7.1c)
(4)case 1
-0.5198a-0.7424b+ 0.4226c=0.7431
-0.6634a+0.3830b+ 0.6428c=0.3420
0.5872a+0.6998b+ 0.4067c=0.8660
，解三聯立方程式，可得[a,b,c]=[0.9169,-0.5984,1.8350]=2.137[-0.4291,0.2800,-0.8857]，
∵=2.137≠1.0，∴[0.9169,-0.5984,1.8350]
非正確解。
case 2
-0.5198a-0.7424b+ 0.4226c=0.7431
-0.6634a+0.3830b+ 0.6428c=0.3420
0.5872a+0.6998b+ 0.4067c=-0.8660
解三聯立方程式，可得
[a,b,c]=[-0.87142,-0.4479,-0.1004]=0.985[-0.8847,-0.4548,-0.5019]
，=0.985≠1.0故[-0.8847,-0.4548,-0.5019]，
即207.20/84.15亦非正確解。
case 3
-0.5198a-0.7424b+ 0.4226c=0.7431
-0.6634a+0.3830b+ 0.6428c=-0.3420
0.5872a+0.6998b+ 0.4067c=-0.8660
解三聯立方程式，可得
[a,b,c]=[-0.2108,-0.9589,-0.1801]=0.996[-0.2119,-0.9604,-0.1810]
∵ a
+b+c≒1.000，如取[a,b,c]=[-0.2119,-0.9604,-0.1810]
，故所求可能平面約為(257.55/79.57)。
case 4
-0.5198a-0.7424b+0.4226c=0.7431
-0.6634a+0.3830b+0.6428c=-0.3420
0.5872a+0.6998b+0.4067c=0.8660
解三聯立方程式，可得
[a,b,c]=[1.5775,-1.1064,1.7553]=-2.606[-0.6052,0.4245,-0.6734]
，亦非正確解，理由同case 1。
(5)經檢討其他組合，其傾向/傾角均與前述四情況之一相同。即正確答案應為
為(257.55/79.57)。如以投影圖解法，則207.21/84.15亦是可能之解。
(6)如第二孔改為150/45時，則可能之答案可能會有二組，請讀者試解之。
(7)圖E2.1為利用電腦程式『鑽探取樣求岩層位態』之計算結果及圖示。
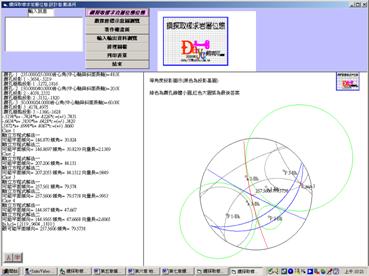
圖E2.1電腦程式『鑽探取樣求岩層位態』計算結果及圖示
2.2.2二個鑽探孔
二個鑽孔之數學解法，與三個鑽孔之解法類似。一般二個鑽孔多建立2個條件方程式，必須利用a+b+c=1之條件方可求解，因此如其有合理解a+b+c一定等於或趨近於1，此與三個鑽孔有解之情況略為不同。
[例題2.2:
二個斜向鑽孔，BH-1(鑽孔方位為210/48) 及BH-2(鑽孔方位為130/34)。量測BH-1及BH-2岩樣中心線與其斜面法線之夾角分別為60°及35°，試求該岩層之可能之位態?
[解答]:
(1)令=1.0，由BH-1及BH-2之鑽探方位及岩樣傾角，可得
-0.5795a-0.3346b+0.7431c=±0.5000
-0.5329a+0.6351b+0.5592c=±0.8192
(2)case 1
-0.5795a-0.3346b+0.7431c=0.5000
-0.5329a+0.6351b+0.5592c=0.8192
將c視為已知解上二式，得：a=-1.0829+1.2064c；b=0.3812+1.1317c
代入a+b+c=1.0，解出c=-0.1482及c=-0.8679，
即[a,b,c]=[0.9401,-0.4007,-0.1482]及[0.0306,-0.4955,-0.8679]，
所求之可能平面為(336.10/81.48)及(274.15/29.79)
case 2
-0.5795a-0.3346b+0.7431c=0.5000，
-0.5329a+0.6351b+0.5592c=-0.819
無實數解
case 3
-0.5795a-0.3346b+0.7431c=-0.5000，
-0.5329a+0.6351b+0.5592c=0.8192
無實數解
case 4
-0.5795a-0.3346b+0.7431c=-0.5000，
-0.5329a+0.6351b+0.5592c=-0.8192
同case 1之解答
(3)圖E2.2為利用電腦程式『鑽探取樣求岩層位態』之計算結果及圖示。
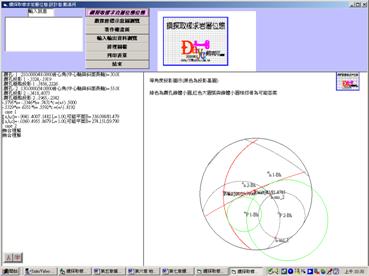
圖E7.2電腦程式『鑽探取樣求岩層位態』計算結果及圖示
2.3.3層面傾角已知
層面傾角(β)已知時，僅剩層面傾向(α)一個未知數，如鑽探孔有2個時，因此如何同時滿足此兩條件方程式，是解答此類問題之關鍵所在。如2鑽探之岩樣位置已知(x,y,z)時，將兩已知(x,y,z)值代入方程式ax+by+cz=d，兩式相減消去d後，與a+b+c=1聯立解(a,b)。如2鑽探之鑽探孔線向/傾沒角及岩心層角已知時，則消除2方程式等號右側常數項後，與a+b+c=1聯立解(a,b)。如只有一鑽探孔，將已知(x,y,z)座標代入方程式ax+by+cz=d求解。限於篇幅，在此僅舉例題2.3，其餘就由讀者自行揣摩。
[例題2.3]:
有一岩層經檢查比對岩樣後判斷：垂直孔BH-1孔口(座標為x
=30.00m，y
=100.00m，z=0.00m)，鑽孔下30.00m處岩層節理(傾角30°)，與另一垂直孔(x
=130.00m，y=150.00m，z=20.00m)，下50.00m處之岩樣節理，屬同一層次，試求該岩層之位態?
[解答]:
(1)兩岩樣取樣位置之連線為岩層平面上之一個向量，其與岩層法線垂直。兩岩樣位置向量為[100,50,40]，即100a+50b+40c=0。
(2)另cos(30°)= ±0.8660，故a+b=0.5
(3)解方程式後經代入原方程式校核後，最可能之岩層平面為334.8579/30及078.2725/30。
(4)圖E7.3為電腦程式『鑽探取樣求岩層位態』計算結果及圖示。
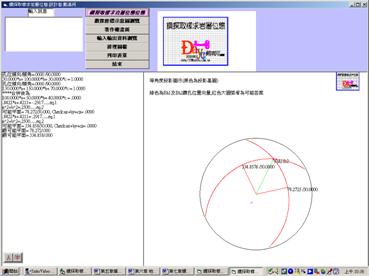
圖E2.3電腦程式『鑽探取樣求岩層位態』計算結果及圖示