|
一、前言
在岩層隧道或地下開挖工程之穩定評估分析工作中,立體等角度(或等面積投影)圖解法,一向扮演了相當舉足輕重不可或缺之角色,尤其是在處理有節理之地下岩層開挖坑頂(Roof)岩楔之穩定簡易評估。上述圖解法步驟簡單易懂,在初步規劃階段頗俱實用性,但如考量岩層之凝聚力或分析岩層隧道側壁(Sidewall)之穩定問題時,則圖解法就變得很複雜而費時費事,以分析坑頂平面與10個節理中任何3個節理所切割之四面體就有120(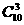 )種組合,與4個節理所切割之五面體則有210種組合,以人工徒手作業幾乎是不可能,縱使可以也可能會掛一漏萬,此時利用電腦其具有快速、正確之優異特性,便相當有競爭力。Cartney, )種組合,與4個節理所切割之五面體則有210種組合,以人工徒手作業幾乎是不可能,縱使可以也可能會掛一漏萬,此時利用電腦其具有快速、正確之優異特性,便相當有競爭力。Cartney,
S.A(1977)、Croney,P.,Legge,T.F.
& Dhalla,A(1978)等,曾發表相關報告以探討岩層隧道之穩定問題,E.Hoek
& E.T.Brown(1980)於渠等所合著之『岩層地下開挖(Underground
Excavation in Rock)』一書中,也在該書第七章專門討論地下開挖破壞機制(Underground
excavation failure mechanisms)。上述報告或書籍立論精闢頗值得一讀,但筆者以為前述第一及第二種報告為一般專業之工程報導,缺乏基本理論之介紹,『岩層地下開挖』雖為工程教科書籍,但只介紹一般圖解法,對初學者而言似乎不夠詳盡,筆者(戴清河(2002))在『岩坡工程學解析』第九章楔形破壞模式分析中雖也有涉及,但篇幅相當有限不夠完整。以P.C及套裝軟體利用普遍之今日,筆者以為往昔之傳統圖解法實有配合現代電腦科技作適度修正、改進以增加圖解法之精確度及解題速度,因此筆者嘗試在本報告中對一般傳統圖解法之製圖作數學理論之解說外,另介紹完全不用投影網之等角度投影圖解法(適合電腦程式製作與CAD繪圖),及三元一次聯立方程式(FORTRAN程式或EXCELL解法)之簡單數學解法以饗讀者,期能收拋磚引玉成效。限於篇幅有關等面積投影圖解法數學推演無法在此詳述,有興趣之讀者可參考『岩坡工程學解析』)。
二、岩層岩層地下開挖
2.1岩層地下開挖工程概述
地下岩層隧道開挖,其破壞機制一般多與其上之覆蓋土(岩)層厚度、周圍土(岩)層分佈及強度情況等因素息息相關,(1)淺層或高度風化岩層下之隧道,其破壞模式多在地下隧道開挖後短時間內發生隧道周圍擠碎(Squeezing)或土(岩)體流動(Flowing)破壞,此類地下隧道之開挖,在工作面進展之同時必須架設大量之安全支撐及襯砌;(2)淺層塊狀多節理岩層隧道開挖,常因覆蓋土(岩)層所產生之岩層應力低,故對隧道之穩定程度影響小,但其較容易因岩楔自重而造成坑頂及側璧岩體坍塌及滑動;(3)少節理輕度風化之鉅積(指岩楔體積比隧道斷面大很多之情況)岩層隧道開挖,如隧道周圍岩層應力小於該等岩層單軸抗壓強度(Uniaxial
compressive strength)之20﹪時,其開挖甚少構成隧道之穩定問題;(4)覆蓋土(岩)層厚度甚大之單一地下隧道開挖或相鄰多坑道之地下礦坑開挖,則易因岩層高應力產生地下隧道或相鄰多坑道之破壞,其模式可能是小規模及少見之剝落(Spalling)、裂片(Slabbing)破壞,或大規模及大量之岩爆(Rockburst))破壞。一般實際地下隧道之開挖,其破壞模式可能是上述二至三種各類別之組合同時發生。破壞模式第(1)類屬土壤隧道開挖問題;第(4)類岩層偏重內部材料應力之探討,限於篇幅本報告在此處所要介紹的是屬岩層不連續面與地下隧道斷面位態三向度相對幾何位置問題之第(2)類破壞模式。
2.1岩層結構控制破壞
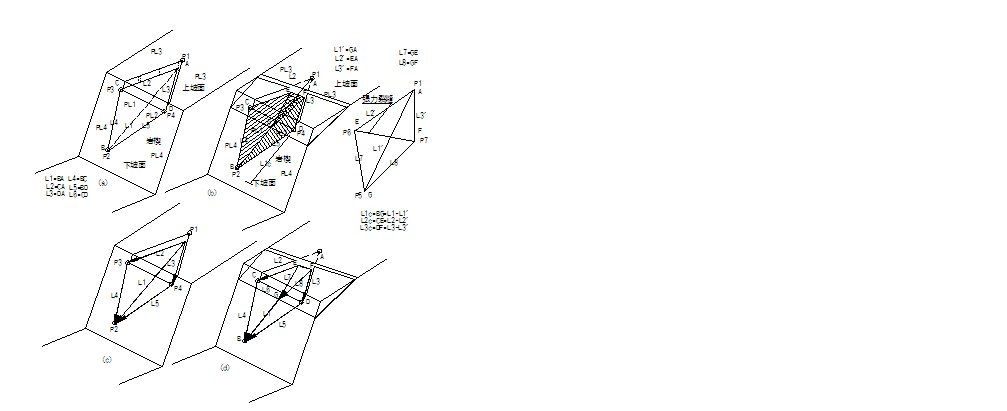
今考慮如圖2.1(a)所示之地下岩層隧道坑頂,其上為兩組走向與隧道行進方向約略平行,即左側傾向/傾角為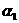 / /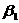 ,右側傾向/傾角為 ,右側傾向/傾角為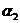 / /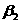 之節理;另有一組與隧道行進方向斜交之節理( 之節理;另有一組與隧道行進方向斜交之節理(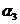 / /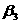 ),其相對之等角度立體投影關係如圖2.1(b)所示,圖中直徑TOT’為第1組節理之走向,弧TAT’為投影大圓,OA為其傾向之投影點,圓心O為三組節理不連續面與坑頂水平面所組成之六面體之頂點,ab為第一、第二組節理之交線;bc為第二、第三組節理之交線;ca為第三、第一組節理之交線;2.1(c)為三組節理平面走向關係示意圖;2.1(d)為三組節理與坑頂平面所切割之岩楔在一般水平面之鳥瞰投影示意圖。圖2.1(b)、(c)及(d)中對應之走向線均互為平行,3.1(b)及(d)中對應之兩平面交線亦均互為平行。圖2.2亦為三組節理平面等角度立體投影圖,2.2(a)圖中三組節理所切割之岩楔,如頂部在隧道坑頂平面之上,則岩楔會因自重而墜落,如頂部在隧道坑頂平面之下則穩定;2.2(b)三組節理與2.2(a)之節理均相差180°,因此其所切割之岩楔與2.2(a)比較,如2.2(a)穩定則2.2(b)不穩定,反之亦然;2.2(c)三組節理中第1、3組節理交點,ca,落在摩擦圓內,故岩楔有沿Oca滑動之可能;3.2(d)三組節理之交點均落在摩擦圓外,故岩楔穩定。圖2.3(a)為圖2.2(a)及2.2(b)兩相似四面體在空間之關係示意圖,圖2.3(a)之兩相似四面體頂點共點,圖2.3(b)為圖2.3(a)旋轉90°之圖示,圖2.3(c)為自由岩坡(有陰影部份)之外伸坡(Overhand
slope)及非外伸坡(Non-overhand
slope)問題。 ),其相對之等角度立體投影關係如圖2.1(b)所示,圖中直徑TOT’為第1組節理之走向,弧TAT’為投影大圓,OA為其傾向之投影點,圓心O為三組節理不連續面與坑頂水平面所組成之六面體之頂點,ab為第一、第二組節理之交線;bc為第二、第三組節理之交線;ca為第三、第一組節理之交線;2.1(c)為三組節理平面走向關係示意圖;2.1(d)為三組節理與坑頂平面所切割之岩楔在一般水平面之鳥瞰投影示意圖。圖2.1(b)、(c)及(d)中對應之走向線均互為平行,3.1(b)及(d)中對應之兩平面交線亦均互為平行。圖2.2亦為三組節理平面等角度立體投影圖,2.2(a)圖中三組節理所切割之岩楔,如頂部在隧道坑頂平面之上,則岩楔會因自重而墜落,如頂部在隧道坑頂平面之下則穩定;2.2(b)三組節理與2.2(a)之節理均相差180°,因此其所切割之岩楔與2.2(a)比較,如2.2(a)穩定則2.2(b)不穩定,反之亦然;2.2(c)三組節理中第1、3組節理交點,ca,落在摩擦圓內,故岩楔有沿Oca滑動之可能;3.2(d)三組節理之交點均落在摩擦圓外,故岩楔穩定。圖2.3(a)為圖2.2(a)及2.2(b)兩相似四面體在空間之關係示意圖,圖2.3(a)之兩相似四面體頂點共點,圖2.3(b)為圖2.3(a)旋轉90°之圖示,圖2.3(c)為自由岩坡(有陰影部份)之外伸坡(Overhand
slope)及非外伸坡(Non-overhand
slope)問題。 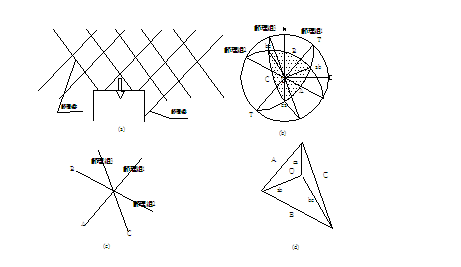
圖2.1岩層隧道位態關係及等角度投影圖
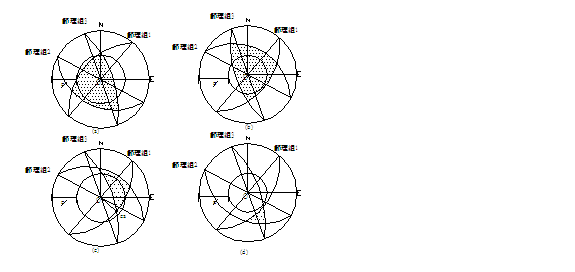
圖2.2隧道等角度投影圖
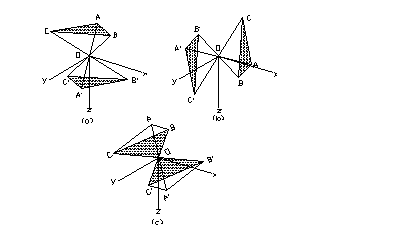
圖2.3傾向相差180之等角度投影關係圖
三、隧道開挖穩定評估
3.1聯立方程式數學解法介紹
如圖3.1之四方形隧道平面,平面i之三度空間平面方程式可以下列方式定義,即a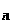 x+a x+a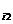 y+a y+a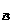 z=a z=a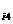 (i=1,n)…………..(4.1), (i=1,n)…………..(4.1),
圖3.1中假定平面1~3(J1~J3)為岩層之不連續面;平面4(T1)為隧道右側平面;平面5(T2)為坑頂平面;平面6(T3)為隧道左側平面;平面7(T4)為隧道底盤平面,則平面1、2、5(i=1,2,5)之交點為A[x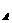 ,y ,y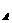 ,z ,z ],平面2、3、5之交點為B[x ],平面2、3、5之交點為B[x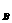 ,y ,y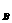 ,z ,z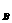 ],平面1、3、5之交點為C[x ],平面1、3、5之交點為C[x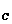 ,y ,y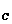 ,z ,z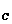 ],平面1、2、3之交點為O[x ],平面1、2、3之交點為O[x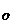 ,y ,y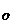 ,z ,z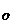 ],平面1、2、4之交點為P[x ],平面1、2、4之交點為P[x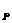 ,y ,y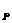 ,z ,z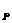 ],平面2、3、4之交點為Q[x ],平面2、3、4之交點為Q[x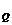 ,y ,y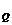 ,z ,z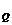 ],平面1、3、4之交點為R[x ],平面1、3、4之交點為R[x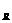 ,y ,y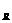 ,z ,z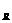 ]……..。如各平面之交點求出後,岩楔之表面積及體積可利用向量之叉積及三重積求解。
岩楔之穩定問題可由各交點座標相對關係判定,而滑動模式可藉岩楔在滑動線兩側平面法線分力之計算值(詳岩坡工程解析第一章及第九章)決定。 ]……..。如各平面之交點求出後,岩楔之表面積及體積可利用向量之叉積及三重積求解。
岩楔之穩定問題可由各交點座標相對關係判定,而滑動模式可藉岩楔在滑動線兩側平面法線分力之計算值(詳岩坡工程解析第一章及第九章)決定。
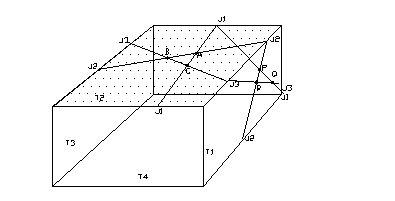
圖3.1隧道斷面示意圖
例題3.1】:
如圖E3.1.1之隧道,三組節理J1:235/50,J2:010/50,J3:085/80均通過(0,0,-17.5)座標點,試評估分析其穩定情況?
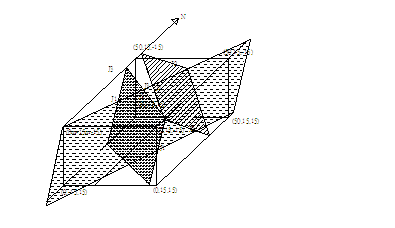
E3.1.1隧道斷面及節理關係示意圖
【解答】:
(1) 圖E3.1.2(a)為三組節理之等角度投影圖,(b)為垂直於隧道方向且經過岩楔頂
點之斷面示意圖。
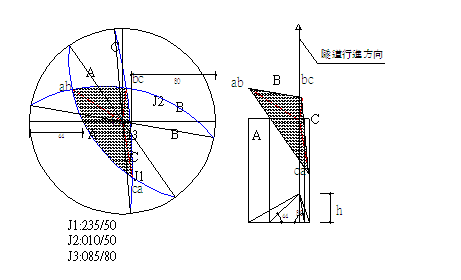
圖E3.1.2節理等角度投影及斷面示意圖,
(2) 節理J1:235/50之單位向上法線向量為[-.043938,
-.062751, -.064279],因其通過(0,0,-17.5),故其平面方程式為:
-0.43938x -0.62751y -0.64279z= 11.24878…….(eq.1),節理J2及J3分別為:0.08583x+0
.98106y -0.17365z= 3.03884……(eq.2),0.75441x+0.13302y-0.64279z=11.24878……….(eq.3),
右側平面(T1)、隧道頂(T2)、左側(T3)、及底盤(T4)分別為:y=15.0(eq……4)
z=-15.0……(eq.5),y=-15.0……(eq.6),及z=15…0……(eq.7)。
(3) 解方程式可得交點P(-9.55606,15.0,
-25.61126 ),Q(120.17330,15.0
126.64530),R(-84.38184,15.0,25.53679),O(0.0,0.0,-17.5),A(2.94531,
-4.62321,-15.0),B(2.08424,0.26015,-15.0),C(-4.90173,0.87135,
-15.0),P’(9.55605
,-15.0,-9.38874),Q’(-120.17330,-15.0,
-161.64530),R’(84.38182,-15.0,-60.53677),A’(38.28898,
-60.10165,15.0),B’(27.09510,3.38200,15.00),C’(-63.72247,
11.32751,15.0)。
(3)O點座標在隧道中央頂部上面2.5公尺,岩楔◇OABC之頂點O在底部△ABC之上方,且底部△ABC各邊之長度均小於隧道之跨度,故岩楔◇OABC會因自重而墜落;岩楔◇OPQR及OP’Q’R,其底部△PQR或P’Q’R’各稜邊多大於隧道高度,因此無產生滑動之安全顧慮。
(4)岩楔◇OABC高為[2.94531,-4.62321,2.5].[0,0,1]=2.5公尺,◇OPQR及OP’Q’R’高為15.0公尺,△OAB之面積為OA、OB兩向量叉積大小絕對值之半,即 =15.631m =15.631m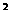 ,△OBC之面積為8.901m ,△OBC之面積為8.901m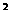 ,△OCA之面積為8.901m ,△OCA之面積為8.901m ,△ABC之面積為16.794m ,△ABC之面積為16.794m ,◇OABC之體積為 ,◇OABC之體積為 =13.995m =13.995m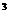 。 。
(5)表E3.1.1為電腦計算之部份報表。
表E3.1.1電腦部份報表。
**** JOINT PLAN DATA****
235.0000/ 50.0000 PROJ TO: (X- .6836)**2+(Y- .9762)**2 =
1.5557**2
10.0000/ 50.0000 PROJ TO: (X- -1.1736)**2+(Y- -.2069)**2 =
1.5557**2
85.0000/ 80.0000 PROJ TO: (X- -.4943)**2+(Y- -5.6497)**2 =
5.7588**2
*** ORIGINAL CORD.[ .0000 .0000 .0000 ]****
PL-2,3,1 [X,Y,Z]= .00000 .00000 -17.50000
PL-1,2,TUN-1 [X,Y,Z]= -9.55605 15.00000 -25.61126
PL-1,3,TUN-1 [X,Y,Z]= -84.38183 14.99999 25.53678
PL-2,3,TUN-1 [X,Y,Z]= 120.17330 15.00000 126.64530
PL-1,2,TUN-2 [X,Y,Z]= 2.94531 -4.62321 -15.00000
PL-1,3,TUN-2 [X,Y,Z]= -4.90173 .87135 -15.00000
PL-2,3,TUN-2 [X,Y,Z]= 2.08424 .26015 -15.00000
PL-1,2,TUN-3 [X,Y,Z]= 9.55606 -15.00000 -9.38874
PL-1,3,TUN-3 [X,Y,Z]= 84.38184 -14.99999 -60.53678
PL-2,3,TUN-3 [X,Y,Z]= -120.17330 -15.00000 -161.64530
PL-1,2,TUN-4 [X,Y,Z]= 38.28898 -60.10165 15.00000
PL-1,3,TUN-4 [X,Y,Z]= -63.72247 11.32751 15.00000
PL-2,3,TUN-4 [X,Y,Z]= 27.09510 3.38200 15.00000
DIPD, & DIP(DEG) OF LINE OR PLANE = 302.500 24.516
LINE- 1,2 [Xi,Yi,Zi]= .4889 -.7674 .4149 302.500/
24.516
235.000/ 50.000 [Px,Py,Pz]= .4381 .6273 .6439
10.000/ 50.000 [Qx,Qy,Qz]= -.7536 -.1319 .6439
DIPD, & DIP(DEG) OF LINE OR PLANE = 169.920 26.664
LINE- 1,3 [Xi,Yi,Zi]= -.8799 .1564 .4488 169.920/
26.664
235.000/ 50.000 [Px,Py,Pz]= .5561 .1359 1.0429
85.000/ 80.000 [Qx,Qy,Qz]= .2154 -.9074 .7386
DIPD, & DIP(DEG) OF LINE OR PLANE = 7.115 49.964
LINE- 2,3 [Xi,Yi,Zi]= .6383 .0797 .7656 7.115/
49.964
10.000/ 50.000 [Px,Py,Pz]= -.8038 .1855 .6508
85.000/ 80.000 [Qx,Qy,Qz]= .1608 -1.0380 -.0261
PT 1- 2-L= 90.6367
PT 2- 3-L= 228.1792
PT 1- 3-L= 200.0294
PT(J&T)- 4 5 PT(J&J)- 1 AF(3D)= 15.631
PT(J&T)- 5 6 PT(J&J)- 1 AF(3D)= 8.901
PT(J&T)- 4 6 PT(J&J)- 1 AF(3D)= 8.091
PT(J&T)- 4 5 PT(J&J)- 6 AF(3D)= 16.794
PT(J&T)- 5 6 1 PT(J&J)- 4 VOL= 13.995
PT(J&T)- 1 2 PT(J&J)- 1 AF(3D)= 873.062
PT(J&T)- 1 3 PT(J&J)- 1 AF(3D)= 1513.672
PT(J&T)- 2 3 PT(J&J)- 1 AF(3D)= 8834.888
PT(J&T)- 1 2 PT(J&J)- 3 AF(3D)= 9014.058
PT(J&T)- 2 3 1 PT(J&J)- 1 VOL= 45070.290
【例題3.2】:
如圖E3.1.2之隧道,三組節理同例題3.1,但隧道方向非指北方向,為由南偏西70°指向北偏東70°,由地質調查資料顯示:J1節理通過(23.646,42.475,1.0),J2節理通過(9.268,42.475,1.0),J3節理通過(91.814,42.475,1.0)等座標點,試評估分析其穩定情況?
【解答】:
(1)三組節理等角度投影同圖E3.1.2(a),圖E3.2.1
為隧道斷面及節理關係示意圖。
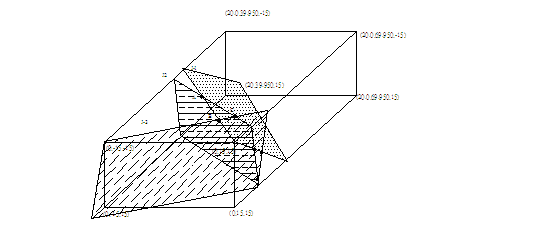
圖E3.2.1隧道斷面及節理關係示意圖
(3)比照例題4.1解方程式可得交點P(11.5676,47.0302,4.7477 ),
Q(12.5676,49.5276,1.6859),R(12.8932,50.4239,6.8997),O(9.7462,50.0311,3.1249),A(-11.6072,83.5492,-15.0),B(45.2835,43.7139,-15.0),C(-5.3645,48.1450,-15.0),P’(18.6069,36.1225,10.6460),Q’(22.8231,47.7065,-3.5447),R’(24.3319,51.8517,20.6201),A’(23.7365,28.0707,15.0),B’(-13.5372,54.1701,15.0),及C’(19.6464,51.2669,15.0)。
(4)O點座標位置在隧道(T1)右側後方8.254m
(50.0311-41.7774),岩楔四面體◇OABC之頂點O在底部三角形△ABC之下方,故岩楔◇OABC不會因自重而墜落;岩楔◇OP’Q’R’因開挖時已移除,因此無產生滑動之安全顧慮;岩楔◇OPQR底部△PQR各稜邊多小於隧道高度,故有產生滑動之安全顧慮,因R點位置最低,故右側岩楔◇OPQR可能是沿OR(J2及J3)交線之楔型滑動破壞,或沿平面J2或J3之平面滑動。
(5)△OPR面積=7.930m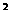 ,△OQR面積=7.736m ,△OQR面積=7.736m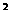 ,◇OABC之體積為=7.895m ,◇OABC之體積為=7.895m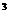 。 。
(6)進一步分析發現岩楔在平面J3法線分力為負值,故岩楔◇OPQR沿平面J2滑動。如J2之凝聚力為0.5t/
m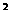 ,摩擦角為30°時,安全係數為1.25,如不考慮凝聚力時安全係數為0.48(tan30°/tan50°)。 ,摩擦角為30°時,安全係數為1.25,如不考慮凝聚力時安全係數為0.48(tan30°/tan50°)。
3.2等角度投影圖解法介紹
依據一般等角度投影之觀念,我們可以知道等角度投影圖上兩平面交線投影之方向為該兩平面交線在x-y平面之方向,利用岩楔之所有稜線其在x-y2D平面之相對位置關係,可以推算出岩楔在3D之相對形狀及位置。如圖3.1(d)中平面A,B,C三個不連續面與一水平面所圍成之四面體岩楔OABC之x-y投影圖上稜線ab,bc及ca等其必與岩楔等角度投影圖(3.1(a))上相對應之交線倆倆平行。圖3.1(d)如某一稜線水平投影尺寸已知,則其他之稜線水平投影尺寸可由圖上直接依比例量測出,再由稜線2D平面尺寸推定3D尺寸及相對位置尺寸。
例題3.3】:
同例題4.1之隧道,試以圖解法評估其穩定情況?
【解答】:
(1)
三組節理之等角度投影圖如圖E4.3.1所示,圖E4.3.1中之座標係由CAD圖上直接丈量出,圖上ab,bc及ca分別為平面A-B,B-C,C-A之交線投影,ad(平面A走向),bd(平面B走向)及cd(平面C走向)分別為平面A,B,C與隧道頂平面交線之投影。
(2)作任一與ab平行之直線為基線,長度取一單位,過基線兩端(Pt1與Pt2)劃與ad與ca之平行線相交於Pt3點,同樣以ab為基線劃與bd與bc之平行線相交於Pt4點,連接Pt3點與Pt4點,則該直線必與cd平行。圖E4.3.2為基線ab為一單位長度時岩楔之x-y平面投影關係圖。
(3)由圖E4.3.2上量測出各稜線之水平投影座標,利用等角度投影基本轉換公
式可以計算出該稜線在空間單位向量座標及長度。以ab基線投影座標
(0.3455,-0.5423)長0.6430為例,換算後之單位向量座標為(4889,-0.7673,0.4150)
,lxy=0.9098,1/
lxy=1.0991﹔ac之1/
lxy=1.1190﹔bc之1/
lxy=1.5546,ad,bd,cd=之1/
lxy均為1.000。
(3)由圖E4.3.2上量測各稜線之水平投影相對長度標示如圖示者,再由各稜線
之水平投影相對長度求取各稜線在3D之相對尺寸。交線ab,bc,ca,ad及bd
在3D之對應長度分別為1.0991,0.5957,1.0158,1.7479,及0.9054。
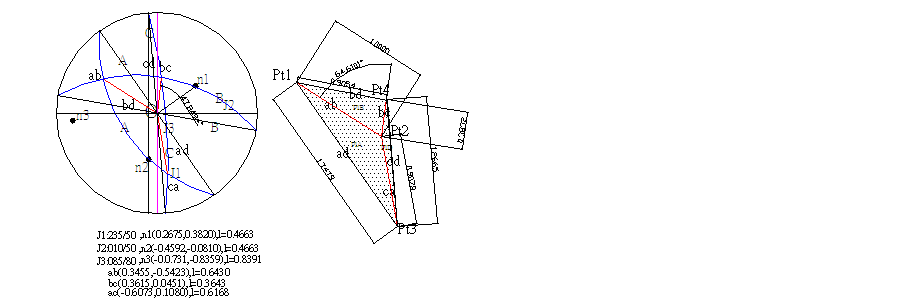 圖E4.3.1等角度投影圖
圖E3.3.2岩楔x-y平面投影圖
圖E4.3.1等角度投影圖
圖E3.3.2岩楔x-y平面投影圖
(4) 再以ab平行之直線為基線,長度仍然為一單位,過基線兩端(Pt1與Pt2)以半
徑1.7479及1.0158劃兩弧相交得Pt3,過基線兩端另以半逕0.9054及0.5957劃相交得Pt4如圖E4.3.3(a)。圖E4.3.3(a)中Pt1-2-3代表平面A,Pt1-2-4代表平面B,Pt2-3-4代表平面C,Pt1-3-4代表隧道頂部平面D。
(5) 如假定Pt2之座標為(0,0,0),則Pt1-2單位向量為[0.5373,-0.8434,0.4561],Pt3-2
為[-0.8937,0.1589,0.4559],Pt2-4為[0.3803,0.0474,0.4562],因平面A,B及C
過定點(0,0,-17.5),即Pt2之座標應平移為(0,0,-17.50),平移後Pt1-2為
[0.5373,-0.8434,-17.5000],Pt3-2為[-0.8937,0.1589,-17.5000],Pt2-4為[0.3803,0.0474,-17.5000]。假定基線實際長度為lf,則岩楔頂點之真正坐標應為Pt2(0,0,-17.5),Pt1-2單位向量為[0.5373lf,-0.8434lf,0.4561lf],Pt3-2為[-0.8937lf,0.1589lf,0.4559lf],Pt4-2為[0.3803lf,0.0474lf,0.4562lf],已知隧道頂部平面z=-15.0,故lf=2.5/0.4561=5.4814,即Pt1之真正座標
為(2.4952,-4.6229,-15.0000),Pt2之真正座標為(0,0,-17.5),Pt3之真正座標(-4.9014,0.8716,-15.0),Pt4之真正座標為(2.0481,0.2600,-15.000)。
(6) 平面A之面積直接由圖E4.3.3(a)丈量為0.5166*5.4814*5.4814=15.52m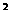 ,平 ,平
面B為0.2694*5.4814*5.4814=8.094m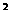 ,平面C不能由圖E4.2.3(a)中三角形Pt2-3-4直接丈量因其非同一個平面,須由圖E4.3.3(b)量測為0.2986*5.4814 ,平面C不能由圖E4.2.3(a)中三角形Pt2-3-4直接丈量因其非同一個平面,須由圖E4.3.3(b)量測為0.2986*5.4814
*5.4814=8.98m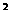 ,岩楔體積為0.5166*0.5963*cos(34.6304)/3*5.4814*504814 ,岩楔體積為0.5166*0.5963*cos(34.6304)/3*5.4814*504814
*504814=13.92 m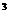 (註34.6304為平面A法線與稜線bc之夾角)。 (註34.6304為平面A法線與稜線bc之夾角)。
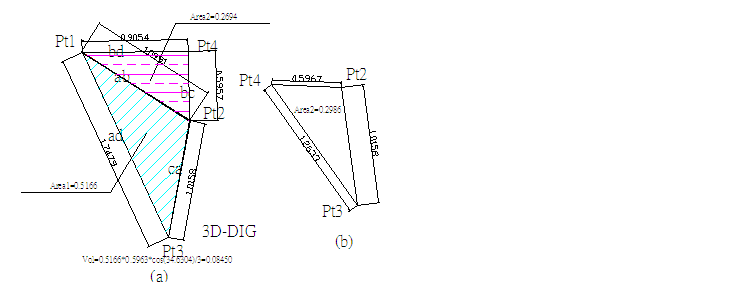
圖E3.3.3岩楔相關位置(3D)圖
(7) 三組節理平面A,B,C與隧道右側平面所切割之岩楔等角度投影如圖E4.3.4(a)所示。圖E4.3.4(a)中之座標,ad,bd及cd分別為三組節理與隧道右側平面交線投影。
(8) 作任一與ab平行之直線為基線,長度取任意值,過基線Pt2作鉛垂線,過基線Pt1分別作平行於ca及bc之平行線與鉛垂線相交於Pt3及Pt4點。丈量各稜線之2D相對尺寸如圖E4.3.4(b),3D相對尺寸如圖E4.3.4(c)所示。
(9) 比照(a)步驟(3)至(7)可以求得Pt1之真正座標為(17.6714,15.0-45.2372),Pt2之真正座標為(0,0,-17.5),Pt3之真正座標為(-29.4081,-15.0,-12.2702),Pt4之真正座標為(12.5046,-15.0,-15.94000)。
(10) 表E4.3.1為利用EXCELL試算表所計算出之三節理與隧道頂部平面所切割之岩楔資料。
(11)
其餘之計算請參考例題4.1。
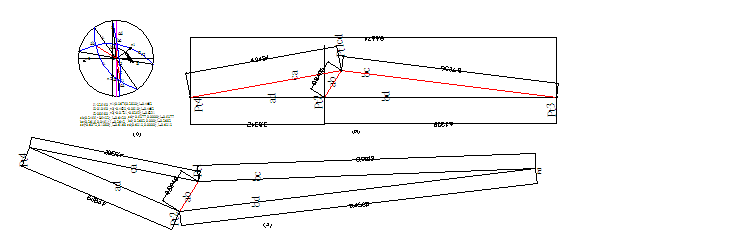
圖E3.2.4岩楔相關位置圖
|
did(deg)? |
dip(deg)? |
nx |
ny |
nz |
ux |
uy |
uz |
xprj(n) |
yprj(n) |
ll(n) |
xprj |
yprj |
|
235.00 |
50.00 |
0.4394 |
0.6275 |
0.6428 |
-0.3687 |
-0.5265 |
0.7660 |
0.2675 |
0.3820 |
0.4663 |
-0.2088 |
-0.2981 |
|
10.00 |
50.00 |
-0.7544 |
-0.1330 |
0.6428 |
0.6330 |
0.1116 |
0.7660 |
-0.4592 |
-0.0810 |
0.4663 |
0.3584 |
0.0632 |
|
85.00 |
80.00 |
-0.0858 |
-0.9811 |
0.1736 |
0.0151 |
0.1730 |
0.9848 |
-0.0731 |
-0.8359 |
0.8391 |
0.0076 |
0.0872 |
|
0.00 |
0.00
|
0.0000 |
0.0000 |
1.0000 |
1.0000 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
0 |
1.0000 |
0.0000 |
|
|
2 vector cross prodoct |
|
|
|
|
|
|
|
|
|
|
|
|
did(deg) |
dip(deg) |
nx(I) |
ny(I) |
nz(I) |
Vx |
Vy |
Vz |
LV |
|
|
|
|
vect.1 |
235.00 |
50.00 |
0.4394 |
0.6275 |
0.6428 |
0.4889 |
-0.7674 |
0.4149 |
1.0000 |
|
|
|
|
vect.2 |
10.00 |
50.00 |
-0.7544 |
-0.1330 |
0.6428 |
|
|
|
|
|
|
|
|
|
unit vector of intesection line |
|
|
|
|
|
|
|
|
|
|
|
|
ix |
iy |
iz |
didi |
dipi |
didf(deg) |
dipf(deg) |
|
chk |
|
xprj |
yprj |
|
case1 |
0.4889 |
-0.7674 |
0.4149 |
-57.50 |
24.52 |
302.50 |
24.52 |
|
0.00
|
90.00 |
0.3455 |
-0.5423 |
|
case2 |
-0.4889 |
0.7674 |
-0.4149 |
-57.50 |
24.52 |
302.50 |
24.52 |
|
0.00
|
90.00 |
|
|
|
|
did(deg) |
dip(deg) |
nx(I) |
ny(I) |
nz(I) |
Vx |
Vy |
Vz |
LV |
|
|
|
|
vect.1 |
10.00 |
50.00 |
-0.7544 |
-0.1330 |
0.6428 |
0.6075 |
0.0758 |
0.7287 |
0.9518 |
|
|
|
|
vect.2 |
85.00 |
80.00 |
-0.0858 |
-0.9811 |
0.1736 |
|
|
|
|
|
|
|
|
|
unit vector of intesection line |
|
|
|
|
|
|
|
|
|
|
|
|
ix |
iy |
iz |
didi |
dipi |
didf(deg) |
dipf(deg) |
|
chk |
|
xprj |
yprj |
|
case1 |
0.6383 |
0.0797 |
0.7656 |
7.11
|
49.96 |
7.11
|
49.96 |
|
0.8226 |
34.6534 |
0.3615 |
0.0451 |
|
case2 |
-0.6383 |
-0.0797 |
-0.7656 |
7.11
|
49.96 |
7.11
|
49.96 |
|
-0.8226 |
145.3466 |
|
|
|
|
did(deg) |
dip(deg) |
nx(I) |
ny(I) |
nz(I) |
Vx |
Vy |
Vz |
LV |
|
|
|
|
vect.1 |
235.00 |
50.00 |
0.4394 |
0.6275 |
0.6428 |
0.7396 |
-0.1315 |
-0.3772 |
0.8406 |
|
|
|
|
vect.2 |
85.00 |
80.00 |
-0.0858 |
-0.9811 |
0.1736 |
|
|
|
|
|
|
|
|
|
unit vector of intesection line |
|
|
|
|
|
|
|
|
|
|
ix |
iy |
iz |
didi |
dipi |
didf(deg) |
dipf(deg) |
xprj |
yprj |
chk |
|
|
|
case1 |
0.8799 |
-0.1564 |
-0.4488 |
169.92 |
26.66 |
169.92 |
26.66 |
-0.6073 |
0.1080 |
0.0000 |
90.0000 |
|
|
case2 |
-0.8799 |
0.1564 |
0.4488 |
169.92 |
26.66 |
169.92 |
26.66 |
|
|
0.0000 |
90.0000 |
|
|
|
did(deg) |
dip(deg) |
vx(I) |
vy(I) |
vz(I) |
dot |
ang(deg) |
|
|
|
|
|
|
|
235.00 |
50.00 |
0.4394 |
0.6275 |
0.6428 |
0.8226 |
34.65 |
|
|
|
|
|
|
|
|
|
0.6383 |
0.0797 |
0.7656 |
|
|
|
|
|
|
|
|
line |
joint |
xproj? |
yproj? |
lproj? |
z |
x |
y |
l |
lxy |
l/lxy |
l_2D? |
l_2D/lxy |
|
ab |
A,B |
0.3455 |
-0.5423 |
0.6430 |
0.4150 |
0.4889 |
-0.7673 |
1.0000 |
0.9098 |
1.0991 |
1.0000 |
1.0991 |
|
ac |
A,C |
-0.6073 |
0.1080 |
0.6168 |
0.4488 |
-0.8798 |
0.1565 |
1.0000 |
0.8936 |
1.1190 |
0.9078 |
1.0158 |
|
bc |
B,C |
0.3615 |
0.0451 |
0.3643 |
0.7657 |
0.6383 |
0.0796 |
1.0000 |
0.6432 |
1.5546 |
0.3832 |
0.5957 |
|
ad |
A,D |
0.8192 |
-0.5736 |
1.0000 |
-0.0001 |
0.8192 |
-0.5736 |
1.0000 |
1.0000 |
1.0000 |
1.7479 |
1.7479 |
|
bd |
B,D |
0.1737 |
-0.9848 |
1.0000 |
0.0000 |
0.1737 |
-0.9848 |
1.0000 |
1.0000 |
1.0000 |
0.9054 |
0.9054 |
|
cd |
C,D |
0.9962 |
-0.0872 |
1.0000 |
0.0000 |
0.9962 |
-0.0872 |
1.0000 |
1.0000 |
1.0000 |
|
|
|
n1 |
|
0.2675 |
0.3820 |
0.4663 |
0.6427 |
0.4394 |
0.6275 |
1.0000 |
0.7661 |
1.3053 |
|
|
|
n2 |
|
-0.4592 |
-0.0810 |
0.4663 |
0.6428 |
-0.7544 |
-0.1331 |
1.0000 |
0.7660 |
1.3054 |
|
|
|
n3 |
|
-0.0731 |
-0.8359 |
0.8390 |
0.1737 |
-0.0858 |
-0.9811 |
1.0000 |
0.9848 |
1.0154 |
|
|
|
line |
ltpt? |
pt |
x1 |
y1 |
z1 |
ztop |
l*x2 |
l*y2 |
l*z2 |
l |
|
|
|
ab |
1.0991 |
1 |
0.00 |
0.00 |
-17.50 |
-15 |
0.5373 |
-0.8434 |
0.4561 |
5.4814 |
|
|
|
bc |
0.5958 |
2 |
0.00 |
0.00 |
-17.50 |
|
0.0000 |
0.0000 |
0.0000 |
|
|
|
|
ca |
1.0158 |
3 |
0.00 |
0.00 |
-17.50 |
-15 |
-0.8937 |
0.1589 |
0.4559 |
5.4841 |
|
|
|
|
|
4 |
0.00 |
0.00 |
-17.50 |
-15 |
0.3803 |
0.0474 |
0.4562 |
5.4802 |
|
|
|
|
x |
y |
z |
|
|
|
|
|
|
|
|
|
|
|
2.9452 |
-4.6229 |
-15.000 |
|
|
|
|
|
|
|
|
|
|
|
0.0000 |
0.0000 |
-17.500 |
|
|
|
|
|
|
|
|
|
|
|
-4.9014 |
0.8716 |
-15.000 |
|
|
|
|
|
|
|
|
|
|
line |
2.0841 |
0.2600 |
-15.000 |
lproj |
ang(2D)? |
A |
B(=z) |
ang(3D) |
|
|
|
|
|
|
n1 |
0.2675 |
0.3820 |
0.4663 |
47.85 |
0.7660 |
0.6428 |
34.6304 |
|
|
|
|
|
bc |
2,3 |
0.3615 |
0.0451 |
0.3643 |
|
0.6433 |
0.7656 |
|
|
|
|
|
[例題3.4]:
在一個有三個不連續面存在之隧道開挖設計工程:平面PL-1之傾向及傾角為(235/45);PL-2之傾向及傾角為(125/45);PL-3之傾向及傾角為(000/45),三個不連續面岩層之內摩擦角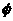 均為30d,粘聚力C均為0.00t/m 均為30d,粘聚力C均為0.00t/m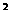 ,岩石之單位重量為2.70t/m ,岩石之單位重量為2.70t/m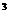 。開挖後側壁平面之傾向/傾角為(170/90,不是外伸坡),隧道中心線之走向及傾角為080/45,隧道高度H=10.0m,試分析檢討其穩定情況? 。開挖後側壁平面之傾向/傾角為(170/90,不是外伸坡),隧道中心線之走向及傾角為080/45,隧道高度H=10.0m,試分析檢討其穩定情況?
[解答]:
(1)計算岩楔各邊之面積、體積及重量
(a)聯立方程式求解
PL-1之單位法線(朝下)n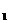 =[-0.4056,-0.5792,-0.7071] =[-0.4056,-0.5792,-0.7071]
PL-2之單位法線(朝下)n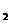 =[-0.4056,0.5792,-0.7071] =[-0.4056,0.5792,-0.7071]
PL-3之單位法線(朝下)n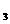 =[0.7071,0.0000,-0.7071] =[0.7071,0.0000,-0.7071]
PL-4之單位法線(朝下)n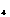 =[-1.0000,0.0000,0.0000] =[-1.0000,0.0000,0.0000]
(b)代入平面方程式ax+by+cz=d公式中,可得
-0.4056x-0.5792y-0.7071z=d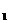 ,-0.4092x+5792y-0.7071z=d ,-0.4092x+5792y-0.7071z=d
0.7071x+0.0000y-0.7071z=d ,-1.0000x+0.0000y+0.0000z=
d ,-1.0000x+0.0000y+0.0000z=
d
(c)參考圖E4.4.1,如令PL-1、PL-2及PL-3三不連續面之交點
 圖E3.4.1楔型滑動破壞示意圖
圖E3.4.1楔型滑動破壞示意圖
P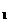 (x (x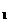 ,y ,y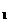 ,z ,z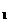 )=
P )=
P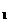 (0.0000,0.0000,0.0000)
,代入其對應之平面方程式後,得
d (0.0000,0.0000,0.0000)
,代入其對應之平面方程式後,得
d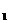 =0.0000,d =0.0000,d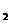 =0.0000,d =0.0000,d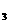 =0.0000 =0.0000
先假設d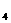 =10.000(可為任意值),解方程式得:P =10.000(可為任意值),解方程式得:P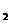 (x (x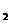 ,y ,y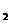 ,z ,z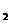 )=
P )=
P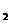 (-11.0154,0,0.58240),P (-11.0154,0,0.58240),P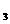 (x (x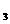 ,y ,y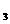 ,z ,z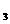 )=
P )=
P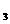 (-7.5850,14.5707,-7.5850) (-7.5850,14.5707,-7.5850)
P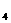 (x (x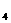 ,y ,y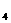 ,z ,z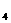 )=
P )=
P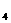 (-15.3555,-29.4976,-15.3555),P (-15.3555,-29.4976,-15.3555),P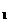 P P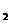 點間之距離 點間之距離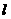 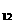 =[(0.0000+10.1543) =[(0.0000+10.1543)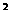 +(0.0000-5.8242) +(0.0000-5.8242)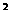 ] ]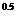 =11.7060m
, =11.7060m
,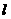 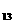 =18,0934m, =18,0934m,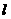 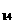 =36.6291m, =36.6291m,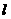 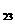 =19.9679m, =19.9679m,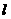 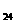 =36.6844m, =36.6844m,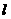 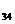 =45.4179m, =45.4179m,
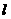 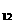 單位向量為[-10.1543,0.0000,5.8242]/11.7060 單位向量為[-10.1543,0.0000,5.8242]/11.7060
=[0.8674,0.000,0.4975],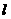 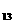 為
[-0.4192,0.8053,-0.4192], 為
[-0.4192,0.8053,-0.4192],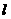 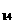 為
[-0.492,-0.8053,-0.192], 為
[-0.492,-0.8053,-0.192],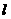 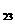 為
[-0.1287,-0.7297,0.6715], 為
[-0.1287,-0.7297,0.6715],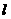 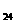 為[0.1418,0.8041,0.5774] 為[0.1418,0.8041,0.5774]
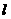 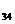 為
[0.1711,0.9703,0.1711] 為
[0.1711,0.9703,0.1711]
(d)岩楔尺寸修正
由隧道行進方向及高度關係(圖E4.2.2),岩楔側面(即隧道側璧)三邊之真正長度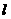 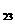 、 、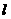 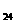 及 及
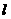 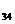 中最大一邊之邊長,其在垂直於隧道行進方向單位向量(圖E4.4.2之n)之投影長度,應等於或小於隧道高度時,岩楔方有可能因重力作用,而向外向下擠入隧道內而滑動。否則岩楔會因體積太大,被隧道側璧阻擋而卡住。隧道中心線之線向及傾角為080/45,n之單位向量為 中最大一邊之邊長,其在垂直於隧道行進方向單位向量(圖E4.4.2之n)之投影長度,應等於或小於隧道高度時,岩楔方有可能因重力作用,而向外向下擠入隧道內而滑動。否則岩楔會因體積太大,被隧道側璧阻擋而卡住。隧道中心線之線向及傾角為080/45,n之單位向量為
n=[cos(80)sin(45),sin(80)sin(45),-cos(45)]=[0.1228,0.6964,-0.7071],
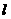 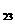 在n之投影長度為: 在n之投影長度為:
19.968[-0.1287,-0.7297,0.6715]•[0.1228,0.6964,-0.7071]=-19.94m
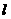 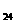 在n之投影長度為: 在n之投影長度為:
36.684[0.1418,0.8041,0.5774]•[0.1228,0.6964,-0.7071]=6.20m
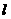  在n之投影長度為: 在n之投影長度為:
54.418[0.1711,0.9703,0.1711]•[0.1228,0.6964,-0.7071]=26.15m,
三者之最大長度為26.15m,故修正係數為10.0/26.15=0.3824,即
P P P 點間正確之距離 點間正確之距離  =11.7060×0.3824=4.477m, =11.7060×0.3824=4.477m,  =18.0924m×0.3824=6.920m, =18.0924m×0.3824=6.920m,  =36.6291m×0.3824=14.009m, =36.6291m×0.3824=14.009m,  =19.9679m×0.3824=7.637m, =19.9679m×0.3824=7.637m,  =36.6844m×0.3824=14.030m, =36.6844m×0.3824=14.030m,  =45.4179m×0.3824=17.370m,各點之正確座標為 =45.4179m×0.3824=17.370m,各點之正確座標為
P (0.0000,0.0000,0.0000),
P (0.0000,0.0000,0.0000),
P (-3.8835,0.0000,2.2275) (-3.8835,0.0000,2.2275)
P (-2.9009,5.5726,-2.9009),P (-2.9009,5.5726,-2.9009),P (-5.8727,-11.2814,-5.8727) (-5.8727,-11.2814,-5.8727)
(2).岩楔之穩定判定:
觀察岩楔各頂點座標發現P 點之座標z值為正,且大於P 點之座標z值為正,且大於P 點之z值,而P 點之z值,而P 、
P 、
P 點之座標z值為負,故P 點之座標z值為負,故P 在P 在P 之下方,而P 之下方,而P 、
P 、
P 點在P 點在P 之上方。故岩楔較有可能沿P 之上方。故岩楔較有可能沿P P P 方向滑動,即由P 方向滑動,即由P 向P 向P 滑動。圖E4.4.3為岩楔在x-y平面投影圖,P 滑動。圖E4.4.3為岩楔在x-y平面投影圖,P 在下故為非外伸坡無誤。 在下故為非外伸坡無誤。
岩楔各邊之面積及岩楔之體積:
A =∣ =∣  × ×  ∣/2=15.303
m ∣/2=15.303
m , ,

圖E3.4.2隧道高度、跨度與不連續面關係示意圖

圖E3.4.3x-y,y-z,x-z投影圖
A =30.979m =30.979m ,岩楔1-2-3-4體積,為P ,岩楔1-2-3-4體積,為P 頂點,P 頂點,P P P 、
P 、
P P P 及
P 及
P P P 為稜邊之岩楔體積, 為稜邊之岩楔體積,
V= ÷6=66.66m ÷6=66.66m
岩楔之重量W=66.66×2.70=180.00
t,i.e
W=[0.00,0.00,180.00]
h =(0.000+2.2275)/2=1.1137m =(0.000+2.2275)/2=1.1137m
U = = h h A A /3=1.0.1.1137.15.303/3=5.681t,即U /3=1.0.1.1137.15.303/3=5.681t,即U =
5.681[-0.4056,
-0.5792, -0.7071 ],U =
5.681[-0.4056,
-0.5792, -0.7071 ],U = = h h A A /3=11.501t,即U /3=11.501t,即U ==
11.501[ -0.4056,0 .5792, -0.7071 ] ==
11.501[ -0.4056,0 .5792, -0.7071 ]
(3).安全係數計算
case (a):
常時無地震及地下水
R=W=[0.00,0.00,180.00]
  之單位向量為
[-0.8674,0.000,0.4795],故W沿 之單位向量為
[-0.8674,0.000,0.4795],故W沿  滑動方向之分 滑動方向之分
力T之大小T,為[0.00,0.00,180.00]•[-0.8674,0.000,0.4975]=89.55
t,即T=89.55[-0.8674,0.000,0.4795]=[-77.6757,0.000,42.9392],如假定垂直於  之W分向量為N,則 之W分向量為N,則
N=W-T=[74.86,0.00,138.61],如假設N在不連續平面PL-1及PL-2單位法線n 及n 及n 之分量為N 之分量為N 及N 及N ,即N ,即N n n +N +N n n =
N ,i.e =
N ,i.e
N [0.4056,0.5792,0.7071]+N [0.4056,0.5792,0.7071]+N [0.4056,-5792,0.7071]= [0.4056,-5792,0.7071]=
[77.68,0.00,137.06],故解出
N =
N =
N =95.77
t =95.77
t
抵抗滑動之抗力=c A A +c +c A A +
N +
N tan( tan(  )+N )+N tan( tan(  ) )
=0.00+0.00+95.77•0.5774+95.77•0.5774=110.58
安全係數Fs=
F /F /F =110.58/89.55=1.235 =110.58/89.55=1.235
case (b):
常時無地震有地下水
合力R=W+U +U +U = =
[0.00,0.00,180.00]+
5.681[-0.4056,
-0.5792, -0.7071 ]
+11.501[-0.4056,0.5792,-0.7071 ]=168.019[-0.0415,0.0201,0.9989],則依上述方式可求,F =100.66t,F =100.66t,F =89.55t,Fs=1.124 =89.55t,Fs=1.124
(4).有關其餘詳細計算及外伸坡隧道岩楔穩定計算請參考岩坡工程學解析一書。
四、結論及建議
(1)等角度投影不用投影網之直接作圖法,配合EXCELL試算表做基本資料計算,則圖解法相當簡便快速,如能用CAD製圖就像如虎添翼,大大提高圖解速度與精度。
(2)本報告所介紹之等角度投影不用投影網之直接作圖法應用範圍廣泛︰諸如(a)地質鑽探求地層位態,(b)岩楔穩定問題,(c)線性地質構造線地層位態等均適用之。
(3)例題4.3所推介之圖解法與坊間所刊登過之一般圖解法大異其趣,其主要觀念係利用(a)岩楔稜線所圍繞形狀,不論是在2D或3D均必須是閉合之觀念,(b)等角度投影圖上任意兩平面之交線(即岩楔之稜線)與岩楔在x-y平面對應之稜線兩兩平行。此類似之圖解法適用在不連續面個數無限大各別岩楔之穩定分析,如需檢討多數節理組與隧道頂部平面或側壁平面穩定問題因需分析可能滑動或落盤之岩楔數量甚多,此時圖解法就不適合。
(4)本報告所介紹之聯立方程式解法,解法簡單迅速,不單可以利用求出之相對座標值以繪製立體之岩楔形狀,亦可以根據相對座標判定岩楔之破壞模式及研判是否屬外伸坡。如利用EXCELL求解時,可以在線上直接觀察運算過程,亦可以利用EXCELL所提供之工具直接繪製岩楔在x-y,y-z,x-z之平面投影圖,一舉數得值得推廣。
(5)一般地下電廠開挖或大斷面之隧道施工,可以利用導坑開挖所取得之地層位態資料,解聯立方程組以預測同路段之相鄰斷面或其他前進斷面之穩定情況(請詳筆者另一報告【多節理之地下開挖穩定分析及落盤預估】),可以隨時掌握機先以降低施工之危險性。
|

