

|
|
1.
Introduction
Most Geologists and
Geotechnical Engineers are familiar with the use of Spherical
projections for the presentation and analysis of structural geology
data, but they may not understand completely the theory foundation of
analytical methods. In order to assist such readers, the principles and
uses of Equal angle and equal area projections are discuss
comprehensively in this papers. In addition, methods for projection
plotting by computer are introduced hereafter. Before talking about
Equal angle and equal area projections, let’s go back to basic
principles. To keep things concrete, we’ll talk the well known three
dimensional plane equation ax+by+cz=d.
2. Review
of space plane
We will use the right-handed
rectangular coordinate system (Cartesian coordinate system) in this
paper. The positive x-axis directs toward the north direction, y-axis
toward the east direction, while z-axis downward. The angle on x-y plane
(orientation a line) is measured beginning from the x-axis in a
clockwise sense, while the inclined angle is measured from x-y plane
downward.
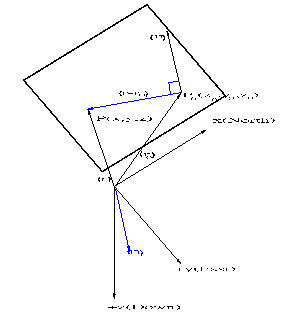
Figure 2.1
In three dimensional
spaces(3D) we can determine a unique plane by specifying a point in the
plane and a vector perpendicular to the plane (Figure 2.1). A vector
perpendicular to a plane is called a normal vector to the plane.
Suppose
that we want to find an equation of the plane passing through a given
point through P (x (x ,y ,y ,z ,z )
and orthogonal to the normal vector n=<a,b,c>. We define two
vectors r )
and orthogonal to the normal vector n=<a,b,c>. We define two
vectors r and
r as and
r as
r =<
x =<
x ,y ,y ,z ,z >
and r=<x,yz> >
and r=<x,yz>
It should
evident obviously from above figure to show that the plane consist
precisely of these points P(x,y,z) for which the vector (r- r )
is perpendicular to n; and be expressed as equation )
is perpendicular to n; and be expressed as equation
n?(r-
r )=0
(1) )=0
(1)
,or
expressed the vector equation in terms of components as
<a,b,c>?<x-x ,y-y ,y-y ,z-z ,z-z >=0
(2) >=0
(2)
From
which we get
a( x-x )+b(y-y )+b(y-y )+c(z-z )+c(z-z )=0
(3) )=0
(3)
This is
called the point-normal form of the equation of a plane.
If
preferred, this equation can be rewritten in the general form as
ax+by+cz
=a x +by +by +cz +cz
denotes
d= ax +by +by +cz +cz ,
we obtain ,
we obtain
ax+by+cz=d
,or
<a,b,c>?<x,y,z>=d
(4)
In
spherical coordinate system (Figure 2.2), if we set the radius length of
the sphere equal to 1.0, since (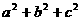 =1.0)
and =1.0)
and 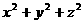 =1.0),
then n=< a,b,c >, r=<x,y,z>. Here n is called unit normal
vector, and r is unit poison vector of the plane ax+by+cz=d. Because
the dot products of two unit vector n?r
equal to Cos( =1.0),
then n=< a,b,c >, r=<x,y,z>. Here n is called unit normal
vector, and r is unit poison vector of the plane ax+by+cz=d. Because
the dot products of two unit vector n?r
equal to Cos(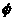 ) )
n?r=
Cos(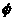 )
(5) )
(5)
,where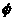 is
the angle between these two unit vectors. The vector form of a plane is
the angle between these two unit vectors. The vector form of a plane
n?r=
Cos(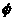 )
play a very important rolls in the spherical projection field. If we
denote a unit sphere as( )
play a very important rolls in the spherical projection field. If we
denote a unit sphere as(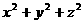 =1.0),
and it’s center at O(0,0,0), then the unit normal vector and unit
position vector all start from spherical center. Suppose ,we think two
unit vector dot products ( n?r)
as any unit position vector r rotate about the unit normal vector n in
clockwise sense 360°,
then the trace of this rotating locus is a circle with center at
o(ad,bd,cd) shown in figure 2.2, and a radius(oa in figue 2.2) equal to
Sin( =1.0),
and it’s center at O(0,0,0), then the unit normal vector and unit
position vector all start from spherical center. Suppose ,we think two
unit vector dot products ( n?r)
as any unit position vector r rotate about the unit normal vector n in
clockwise sense 360°,
then the trace of this rotating locus is a circle with center at
o(ad,bd,cd) shown in figure 2.2, and a radius(oa in figue 2.2) equal to
Sin(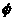 ).
It is not difficult to verify that any unit position vector r<x,y,z>
in the plane which passing O(0,0,0), ie. n?r=d=0,
then the corresponding parallel unit position vector r’=<ad+xSin( ).
It is not difficult to verify that any unit position vector r<x,y,z>
in the plane which passing O(0,0,0), ie. n?r=d=0,
then the corresponding parallel unit position vector r’=<ad+xSin(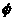 ),bd+ySin( ),bd+ySin(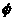 ),cd+zSin( ),cd+zSin(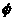 )>,
which lying on the unit spherical surface. If any unit position vector
in a plane passing O(0,0,0) is given ,then the corresponding unit vector
in the intersected circle can be calculated by )>,
which lying on the unit spherical surface. If any unit position vector
in a plane passing O(0,0,0) is given ,then the corresponding unit vector
in the intersected circle can be calculated by
r’=<ad+xSin(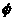 ),bd+ySin( ),bd+ySin(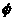 ),cd+zSin( ),cd+zSin(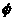 )>
6 )>
6
The trace
of intersection of unit sphere and a plane can solve by rotating unit
position vector r’ about unit normal vector in required scene 360°.
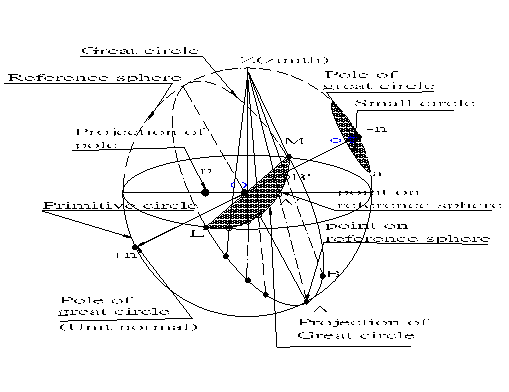
Figure 2.2
An
inclined geological plane is defined by its orientation with respect the
north which may be defined by strike or dip direction of the plane and
defined by its inclination or dip to the horizontal. The strike of a
plane is the trace of the intersection of that plane with a horizontal
surface. A dip direction is the orientation which perpendicular to plane
strike.
In
structural geology, when people concern only the attitude (strike/dip or
dip
direction/dip) of a structural plane, so we can assume d=0, While in
geological weakness plane displacement, rock stability analysis (rock
wedge volume computing) and drill-core analytical calculation problem
etc., d can not be assumed all zero for concerned planes (for example,
if a rock wedge is cut by 5 planes (five equations), to calculate the
volume of rock wedge, for conveniently, we can set three of them with
d=0 only)
If we use
the spherical coordinate system, the plane with a dip direction
(α)
and a dip angle (β), then the downward unit
normal vector can be defined as
n= <a,b,c>=<
- Cos(α)sin(β),Cos(β)Cos(α)Sin(β),Cos(β)>
7
Any unit
position vector on the plane with a trending (p) and plunging (q) is
r=
<x,y,z>=< Cos(p)Cos(q), Sin(p)Cos(q),Sin(q)>
8
and the
plane equation can be expressed as following:
<a,b,c>?<x,y,z>=-Cos(α)Cos(β)Cos(p)sin(q),-Sin(α)Cos(β)Cos(p)Sin(q)
+Sin(β)Cos(q)=d=cos(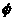 )
9 )
9
Any two
vectors <u>=<u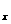 ,u ,u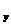 ,u ,u >
and <v>=< v >
and <v>=< v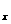 ,v ,v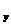 ,v ,v >
lying on the plane, >
lying on the plane,
Then, the
unit normal vector of the plane are defined as the vector cross
products
<u>×<v>=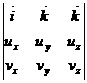 / /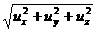 / /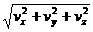 10
10
Where,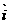 , ,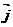 , ,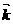 are
the unit vectors along x, y, z axes respectively. are
the unit vectors along x, y, z axes respectively.
The unit
normal vector of a plane passing unit sphere is unique, but the
unit
position vector of the plane can be many, so a plane rotate about a
axis, you can use the unit normal vector to represent this plan, you can
not use the unit dip direction vector to represent this plane, but you
can use two vectors lying in the plane to get the desired plan for
rotation also. The intersection of unit sphere and plane are a three
dimensional circle. If the plane (d=0) is passing unit spherical center,
then their intersection is call great circle, while a plane with d<>0,
its intersection is call small circle. The intersection of a horizontal
plane with reference unit sphere is called primitive circle.
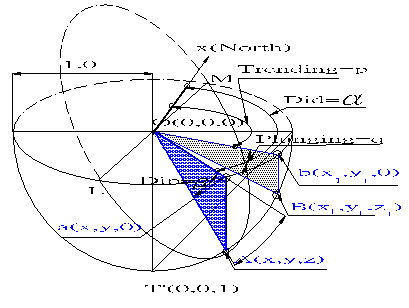
Figure 2.3
As shown
in figure 2.3, any unit position vector r on the plane with a trending
(p, dip direction of a line) and plunging (q, dip angle) should
perpendicular to the plane normal. If the plane with unit normal vector
n=<a,b,c>, and unit position vector r=<x,y,z>. From n?r=cos(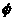 ),by
setting p=p ),by
setting p=p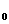 ,
we can solve q values from the following equation ,
we can solve q values from the following equation
aCos(p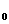 )cos(q)+bSin(p )cos(q)+bSin(p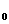 )cos(q)+sin(q)=cos( )cos(q)+sin(q)=cos(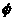 )
11 )
11
So, the
trace of the unit sphere and plane intersection can be calculated by
setting p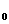 =(β-90)+i* =(β-90)+i*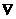 β
(where i=1~n, β
(where i=1~n,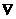 β=180/n
for great circle projection ,and =360/n for small circle projection ) to
solve equation (11) one by one. β=180/n
for great circle projection ,and =360/n for small circle projection ) to
solve equation (11) one by one.
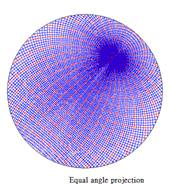
3. Equal
angle projection
The equal
angle projection, also know as Stereographical projection or
Wulff
Projection, is obtained by the method illustrated in th figure 3.1 and
3.2.
The line
AZ from point A(x,y,z) on the unit sphere to the zenith point Z(0,0,-1)
pierces
the unit horizontal (equator) plane at point
 (x (x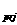 ,y ,y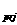 ),
then ),
then
point
 (see
figure 3.2) is a equal angle projection of point A on this unit sphere (see
figure 3.2) is a equal angle projection of point A on this unit sphere
surface.
Since vecctor <ZA> =<x,y,z-1>, vector< >=(
x >=(
x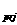 ,y ,y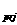 ,0)
,and line ,0)
,and line
 lying
on line ZA, so lying
on line ZA, so
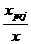 = =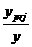 = =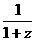 12
12 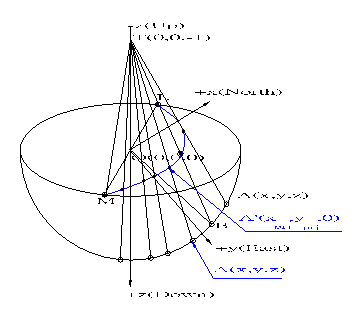
figure 3.1
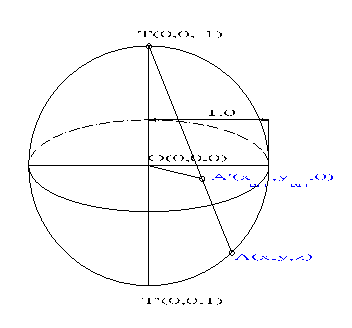
figure 3.2
It
Implies that
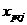 = =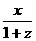 13a
13a
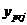 = =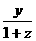 13b
13b
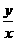 = =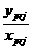 13c
13c
The above
three governing equation are reversible, substitute <x,y,z>=
<
Cos(p)Cos(q), Sin(p)Cos(q),Sin(q)> into equation 13c, we get
Tan(p)=
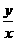 = =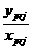 14a
14a
Sin(p)=±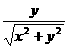 14b
14b
Cos(p)=
±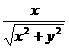 14c
14c
From x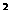 +y +y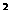 =1-z =1-z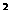 ,
getting ,
getting
Sin(q)=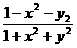 15a
15a
Cos(q)=±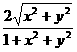 15b
15b
Substituting equations (13) and (14) into the general plan equation
ax+by+cz=d=Cos(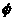 ),
we obtained ),
we obtained
( x-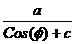 ) )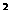 +(y- +(y-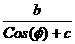 ) )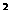 =( =(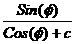 ) )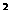 16
16
If we
denote (h,k) as center of a small projection circle, r as radius , then
h=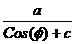 17a
17a
k=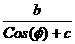 17b
17b
r=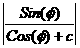 17c
17c
When
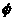 =90,
then the small circle projection change to great circle projection =90,
then the small circle projection change to great circle projection
(x-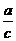 ) )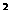 +(y- +(y-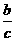 ) )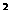 =( =(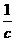 ) )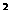 18
18
It means
that the great circle equal angle projection is with a arc with center
at (h,k)=( 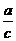 , ,
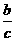 ),
and a radius r= ),
and a radius r=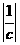 ,
If the dip plane(α/β)
given ,we can obtain the following great circle projection formulas: ,
If the dip plane(α/β)
given ,we can obtain the following great circle projection formulas:
h=-Cos(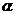 )Tan( )Tan(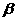 )
19a )
19a
k= Sin(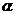 )Tan( )Tan(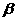 )
19b )
19b
r=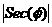 19c
19c
if we
denote four unit position vectors in the attitudes at (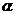 -90)/0,
( -90)/0,
(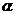 / /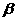 )
, )
, 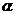 +90)/0
, and unit normal vector projection coordinates as (x +90)/0
, and unit normal vector projection coordinates as (x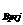 ,y ,y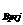 ),
(x ),
(x ,y ,y )
,(x )
,(x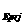 ,y ,y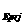 ),
and (x ),
and (x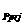 ,
y ,
y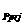 )
respectively ,then )
respectively ,then
(a)at
dip direction/dip=(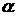 -90/0) -90/0)
x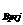 =
Sin( =
Sin(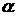 )
20a )
20a
y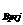 =
-Cos( =
-Cos(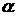 ))
20b ))
20b
(b)at
did direction/dip=(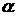 /β)
and r<x,y,z> /β)
and r<x,y,z>
x = =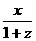 =Cos(α)Cos(β)/[1+Sin(β)]=Cos(α)Tan(pi/4-β)
20c
y =Cos(α)Cos(β)/[1+Sin(β)]=Cos(α)Tan(pi/4-β)
20c
y = =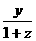 =Sin(α)Cos(β)/[1+Sin(β)]=Sin(α)Tan(pi/4-β) 20d =Sin(α)Cos(β)/[1+Sin(β)]=Sin(α)Tan(pi/4-β) 20d
(c)
at did direction/dip=(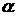 +0/0) +0/0)
x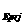 =
-Sin( =
-Sin(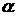 )
20e )
20e
y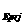 =
Cos( =
Cos(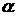 )
20f )
20f
(d))at
did direction/dip=(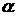 /β)
and n=<a,b,c> /β)
and n=<a,b,c>
x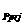 = =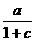 =Sin(α)Tan(β/2)
20g =Sin(α)Tan(β/2)
20g
y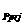 = =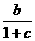 =Cos(α)Tan(β/2)
20h =Cos(α)Tan(β/2)
20h
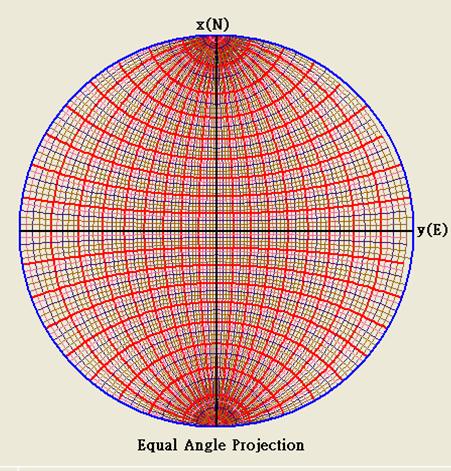
Figure 3.4
If
we set did direction did=90°,
dip angle dip=0°~ 180° for
every 2° interval, and set did=0°,dip=0°
and 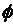 =0°~
180° for every 2°
interval, we can plot the great circle shown in figure 3.4. =0°~
180° for every 2°
interval, we can plot the great circle shown in figure 3.4.
3.1
Measurement of the angle of two vectors from equal angle projection
As
mention before, the equal angle projection formula of a unit vector are
x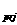 = =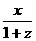 and
y and
y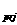 = =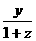 ,suppose
two unit vectors are denoted by v ,suppose
two unit vectors are denoted by v =<v =<v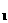 ,v ,v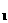 ,v ,v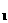 >,and
v >,and
v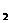 =<v =<v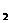 ,v ,v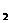 ,v ,v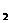 >,
and their equal angle projection coordinates of great circle are denoted
as (x >,
and their equal angle projection coordinates of great circle are denoted
as (x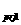 ,y ,y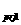 )
,(x )
,(x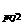 ,
y ,
y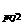 )
respectively , then the angle( )
respectively , then the angle(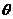 )
between these two vector in 3d is )
between these two vector in 3d is
cos(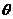 )=v )=v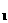 v v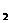 +v +v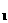 v v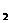 +v +v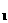 v v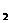 21
21
This
angle can measure from the projection map. If we assume t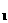 =(1+x =(1+x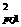 +y +y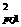 ),
t ),
t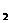 =(1+x =(1+x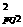 +y +y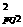 ),
then ),
then
cos(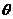 )= )=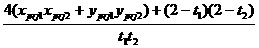 22
22
If denote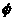 =Cos =Cos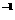 (d)
is the angle of small circle cone ,then the angle between
two
vectors in space is (d)
is the angle of small circle cone ,then the angle between
two
vectors in space is
sin(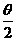 )= )=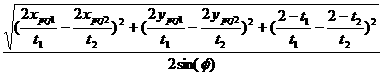 23
23
3.2
Application of equal angle projection
Let the plan P(pole p) strike
N250E and dip35( Dip direction/dip=160/35),It is required to project
this plane by equal angle method. Since the dip direction unit position
vector is r=<-0.7698,0.2802,0.5736> , unit normal is n=
<0.5390,-0.1962,0.8192>, then the great circle projection (x ,y ,y ) )
x = =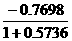 =-0.4892 =-0.4892
y = =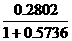 =0.1780 =0.1780
the great
circle center (h,k) and r are
h=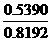 =0.6580 =0.6580
k=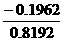 =-0.2395 =-0.2395
r=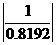 =1.2208 =1.2208
the
normal projection (x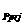 ,y ,y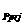 )
is )
is
x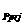 = =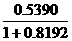 =0.2963 =0.2963
y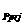 = =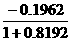 =0.1708. =0.1708.
Since we can easy to calculate
an equal angle projection of center, radius of the great circle and
small circle, so to plot the projection diagram is a easy task of
plotting an arc for great circle, and circle or arc of small circle
projection. The procedures of plotting a small circle projection can be
summarized as follows.
Calculating a unit normal vector of a plane.
(2a) Calculating then
projection coordinate of the three key points at
(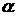 -90)/0, -90)/0,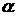 / /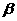 ,
( ,
(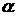 +90)/0). +90)/0).
(2b) Or,
Calculating the small circle projection its center (h,k), and r .
Drawing three points circle,
or a circle with center and radius given.
The
following Excel spreadsheet is designed for calculating and drawing the
small (or great) circle equal angle and equal area projection.
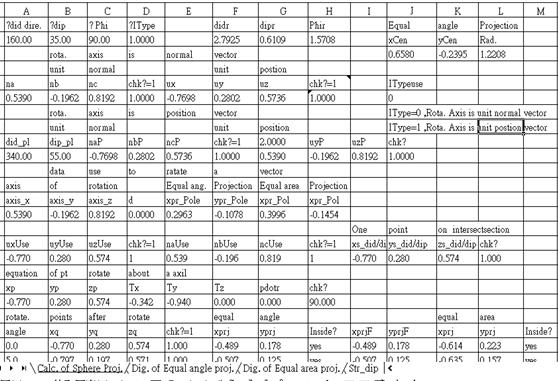
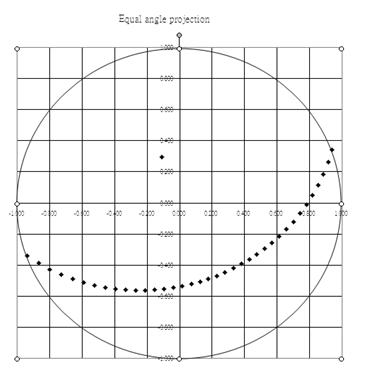
Figure 3.5
3.3
Rotation about an axis inclined axis
Let
the plane P (with
a pole p (with
a pole p strike
N80°E and dip50°S(170/50).
It is required to rotate P strike
N80°E and dip50°S(170/50).
It is required to rotate P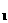 100°
in a clockwise sense(viewed toward the NE) about an axis R trending N40°E
and plunging 30°(40/30). The locus of rotation of
a point projection by graphic method using projection net is time
consuming and tedious, but it is quite easy to compute the rotation of a
3-space point using the rotation matrix transformation, and then project
the rotated point using equation 13. Suppose the axis of rotation is a
line passing point (a,b,c) and parallel to the unit vector <u,v,w>.
After rotating in required sense θ°, if point
after rotation denotes as (x 100°
in a clockwise sense(viewed toward the NE) about an axis R trending N40°E
and plunging 30°(40/30). The locus of rotation of
a point projection by graphic method using projection net is time
consuming and tedious, but it is quite easy to compute the rotation of a
3-space point using the rotation matrix transformation, and then project
the rotated point using equation 13. Suppose the axis of rotation is a
line passing point (a,b,c) and parallel to the unit vector <u,v,w>.
After rotating in required sense θ°, if point
after rotation denotes as (x ,y ,y ,z ,z ),then
(x ),then
(x ,y ,y ,z ,z )
can be defined as )
can be defined as
x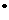 = =
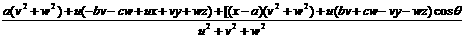
+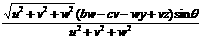
y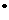 = =
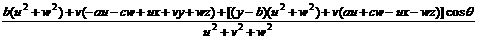
+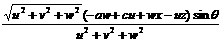
z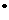 = =
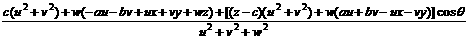
+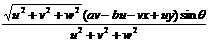 (after
Glenn Murray ,Coloado School of Mines) (after
Glenn Murray ,Coloado School of Mines)
Since the unit normal vector
of plane (170/50) is <0.7544, - 0.1330, 0.6428>, the unit position
vector (40/30) is <0.6634, 0.5567, 0.5>, the unit normal vector after
rotation is <-0.8691, 0.4632,-0.1733>. The corresponding projection
coordinates (figure 3.3) are (0.4422, 0.3711), (0.4592, -0.081),
(0.7408, -0.3949), respectively. Please note here that the sign of z
coordinate of the normal vector (170/50) before and after rotation are
different, then the coordinate of normal vector (170/50) after rotation
should change the sign when applies the projection equation 13 and 20g
,,20h etc. Figure 3.6 shows the results.
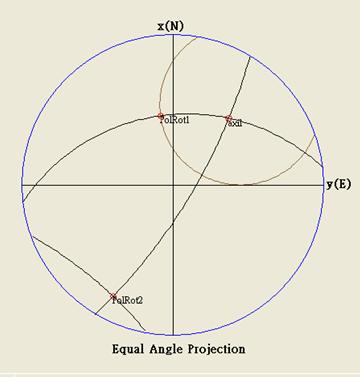
Figure 3.6
Figure 3.7 is an inclined
equal-angle net for rotation a line inclined at 30°
to the plane of projection.

Figure 3.7
4. Equal
area projection
The equal area
projection, also know as Schimidt projection, is
Obtained
by the method illustrated in th figure 4.1. The line TA is from the

Figure 4.1
zenith
point T(0,0,1) to point A(x,y,z) on the unit sphere surface. By swing
Line  A
, which pivoted at A
, which pivoted at  ,
until it lying on the horizontal plane underlying point B(x ,
until it lying on the horizontal plane underlying point B(x ,y ,y ,z ,z ).
Notes here, since the length of any point on unit primitive circle and
its corresponding equal area projection point in the bottom horizontal
is ).
Notes here, since the length of any point on unit primitive circle and
its corresponding equal area projection point in the bottom horizontal
is [point
X(1,0,0)on spherical surface, project on bottom horizontal plane is X [point
X(1,0,0)on spherical surface, project on bottom horizontal plane is X ( ( ,0,-1),
so the max radius of bottom projection circle is ,0,-1),
so the max radius of bottom projection circle is
 .],
so the point of equal area projection mapping on equator horizontal
circle need to reduce .],
so the point of equal area projection mapping on equator horizontal
circle need to reduce .
And, length of TA = .
And, length of TA = = =
= B.
If we denote orthogonal projection of point A is B.
If we denote orthogonal projection of point A is
 (x,y,1),
since length of (x,y,1),
since length of  A= A=
 = = ,
and points ,
and points  ,
A, ,
A, lying
on the same line, by denoting the point coordinates on unit spherical
surface as A(x,y,z), follows the procedures as the equal angle
projection does , we can get the governing equations . lying
on the same line, by denoting the point coordinates on unit spherical
surface as A(x,y,z), follows the procedures as the equal angle
projection does , we can get the governing equations .
x = = 24a
24a
y = = 24b
24b
 = = 24c
24c
The above three governing
equations are reversible.if we denote four unit position vectors in the
attitudes at ( -90)/0,
( -90)/0,
( / / )
, )
, +90)/0
, and unit normal vector projection coordinates as (x +90)/0
, and unit normal vector projection coordinates as (x ,y ,y ),
(x ),
(x ,y ,y )
,(x )
,(x ,y ,y ),
and (x ),
and (x ,
y ,
y )
respectively ,then we can get the following equations )
respectively ,then we can get the following equations
(a) at did direction/dip=[( -90)/0]
and r<x,y,z> -90)/0]
and r<x,y,z>
x =
Sin( =
Sin( )
25a )
25a
y =
-Cos( =
-Cos( )
25b )
25b
(b) at did direction/dip= ( / / )
and r(x,y,z) )
and r(x,y,z)
x = = = = Cos(α)Sin(pi/4-β)
25c Cos(α)Sin(pi/4-β)
25c
y = = = = Sin(α)Sin
(pi/4-β) 25d Sin(α)Sin
(pi/4-β) 25d
(c) at did direction/dip=[( +90)/0] +90)/0]
x =
-Sin( =
-Sin( )
25e )
25e
y =
Cos( =
Cos( )
25e )
25e
(d) at did direction/dip=( /β)
and n<a,b,c> /β)
and n<a,b,c>
x = = = = Sin(α)Sin(β/2)
25g Sin(α)Sin(β/2)
25g
y = = = = Cos(α)Sin(β/2)
26h Cos(α)Sin(β/2)
26h
suppose two unit vectors are
denoted by v =<v =<v ,v ,v ,v ,v >,and
v >,and
v =<v =<v ,v ,v ,v ,v >,
and their equal area projection coordinates of great circle are denoted
as (x >,
and their equal area projection coordinates of great circle are denoted
as (x ,y ,y )
,(x )
,(x ,
y ,
y )
respectively , then the angle( )
respectively , then the angle( )
between these two vector in 3d is )
between these two vector in 3d is
cos( )=v )=v v v +v +v v v +v +v v v 21
21
This angle can measure from
the projection map. If we assume t =(1+x =(1+x +y +y ),
t ),
t =(1+x =(1+x +y +y ),
then ),
then
cos( )= )= 27
27
If denote =Cos =Cos (d)
is the angle of small circle cone ,then the angle between two vectors in
space is in space is sin( (d)
is the angle of small circle cone ,then the angle between two vectors in
space is in space is sin( )= )= 28
28
Because the curve of equal
area projection for small (or great) circle is not a circle (arc), it is
a forth-degree equation in x, y. the graph of the equation is an
elliptic curve. Because it is difficult to find the lengths of semimajor
axis and semiminor axis of an ellipse projection curve, so we can not
draw the projection graph by plotting elliptic curve directly. In this
paper, the author will introduce two methods to plot the small circle
and great circle projection.
1.


3.2
Application of equal angle projection
Let the plan P(pole p) strike
N250E and dip35( Dip direction/dip=160/35),It is required to project
this plane by equal angle method. Since the dip direction unit position
vector is r=<-0.7698,0.2802,0.5736> , unit normal is n=
<0.5390,-0.1962,0.8192>, then
the great circle projection (x ,y ,y ) )
x = = =-0.4892 =-0.4892
y = = =0.1780 =0.1780
the great circle center (h,k)
and r are
h= =0.6580 =0.6580
k= =-0.2395 =-0.2395
r= =1.2208 =1.2208
the normal projection (x ,y ,y )
is )
is
x = = =0.2963 =0.2963
y  = = =0.1708). =0.1708).
Since we can easy to calculate
an equal angle projection of center, radius of the great circle and
small circle, so to plot the projection diagram is an easy task of
plotting an arc for great circle, and circle or arc of small circle
projection. The procedures of plotting a small circle projection can be
summarized as follows.
Calculating a unit normal
vector of a plane.
(2a) Calculating then
projection coordinate of the three key points at ( -90)/0, -90)/0,  / / ,
( ,
( +90)/0). +90)/0).
(2b) Or, Calculating the small
circle projection its center (h,k), and r .
Drawing three points circle,
or a circle with center and radius given.
The following Excel
spreadsheet is designed for calculating and drawing the small (or great)
circle equal angle and equal area projection.

|