ImplicitFunction

2018年12月02日

How to solve an implicit function

Some time you may need to solve an implicit function like x^3+2*x*y^2+x*y^3-x^2*z^2-25=0 in some domain {x,-5~5},{y,-5~5},{z,-5~5},if you don’t have any software package. In this case, you can use the algorithm of finding roots of a polynomial function like a0+a1*x+a2*x^2+a3*x^3+….+an*x^n just to set z=z0,y=y0 to convert the original function to

x^3+ 2*x*y0^2+x*y0^3-z0^2-25=0

,and then solve the cubic function of one variable. In this article, you will learn how to use VBScript control to let client to input the function in character string, and the computer will detect the order of the polynomial function and the compute coefficients of the polynomial automatically.

The key point to solve an implicit function with some domain by solving polynomial function is to find the coefficients of a polynomial function when you assume z=z0 and y=y0.

Hereafter are a snippet codes to find coefficients of a polynomial.

Private Sub FindPolyCoeffLH(eqStIn As String, yIn As Single, zIn As Single, eqStOut As String, nPoly As Integer, Acoeff_0() As Double, Optional iTest As Boolean = False)

'***********************************************

'Please note here function :A(0)x^n+A(1)x^(n-1)+A(2)x^(n-2)+........+A(n)

'if 2x^5+3x^4+2x^3+3x^2+4x+5=0 : then A(0)=2,A(1)=3,A(2)=2,A(3)=3,A(4)=4,A(5)=5

'***************************************************

Dim i As Integer, count As Integer, j As Integer

Dim x As Single, y As Single, z As Integer

Dim ret As Variant

'-----------------------------------------------

Dim st As String

st = eqStIn

ret = FunValue(st, 0, 0, 0)

'List1.AddItem "a(0)=" & ret

st = LCase(st)

st = Replace(st, "x*", "x^1*")

stArray = Split(st, "+", -1, vbTextCompare)

'List1.AddItem St

count = 0

For i = 0 To UBound(stArray)

ReDim Preserve Axyz(0 To count)

Axyz(count) = stArray(i)

'List1.AddItem "i= " & count & " ;Axyz(" & count & ")= " & Axyz(count)

count = count + 1

Next i

'------------------------

count = count - 1

nPoly = -999

For i = 0 To count

For j = 1 To 10

If InStr(Axyz(i), Trim("x^" & j)) And j >= nPoly Then

nPoly = j

End If

Next j

Next i

'List1.AddItem " order of poly= " & nPoly

ReDim Preserve Acoeff_0(0 To nPoly)

Acoeff_0(nPoly) = FunValue(eqStIn, 0, yIn, zIn)

For j = 1 To nPoly

Acoeff_0(nPoly - j) = 0

For i = 0 To count

' MsgBox ("x^" & Trim("x^" & j) & ";axyz= " & Axyz(i))

If InStr(Axyz(i), Trim("x^" & j)) Then

Acoeff_0(nPoly - j) = Acoeff_0(nPoly - j) + FunValue(Axyz(i), 1, yIn, zIn)

End If

Next i

Next j

If iTest Then

For i = 0 To nPoly

List1.AddItem "z= " & zIn & " ;y= " & yIn & " A(" & i & ")= " & Acoeff_0(i)

End If

Dim Fxyz As String

Fxyz = Str(Acoeff_0(0))

For i = 1 To nPoly

Fxyz = Fxyz & Trim("+" & Str(Acoeff_0(i)) & Trim("*x^" & i))

Next i

If iTest Then List1.AddItem Fxyz

eqStOut = Fxyz

End Sub

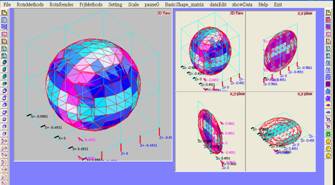
The figure shown as below is the result using the snippet code attached hereafter.

Private Sub ImplicitB(EqIn As String)

'***********************************************

'Please note here function :A(0)x^n+A(1)x^(n-1)+A(2)x^(n-2)+........+A(n)

'if 2x^5+3x^4+2x^3+3x^2+4x+5=0 : then A(0)=2,A(1)=3,A(2)=2,A(3)=3,A(4)=4,A(5)=5

'***************************************************

EyeR = 10

EyeTheta = pi * 0.2

EyePhi = pi * 0.2

m3PProject glPST, m3Perspective, EyeR, EyePhi, EyeTheta, FocusX, FocusY, FocusZ, 0, 1, 0

FactorMaker glPST

Dim nPoly As Integer, Acoeff_0() As Double, i As Long, nans As Integer, Nroots As Integer

Dim EqOut As String, Roots As PolyRoot, xans As Single, count As Long

Dim xp As Single, yp As Single, ptsIn() As pointApi, ptsOut() As pointApi

Dim ptTpt As cadPoint

Dim rgbR As Byte, rgbG As Byte, rgbB As Byte, yFctUse As Single

Dim y As Single, z As Single, countTL As Integer

Dim stColl As New Collection, stArray() As String

Dim xFun() As Single, yFun() As Single, zFun() As Single

Dim ansReal() As Double, ansImag() As Double

Dim time1 As Double

time1 = Timer

EqIn = LCase(EqIn)

If InStr(EqIn, "^") = 0 Then

EqIn = Replace(EqIn, "x", "x^1")

End If

List1.AddItem EqIn

countTL = 0

yFctUse = -1

Set stColl = Nothing

For z = 5 To -5 Step -0.25

count = 0

Erase ptsIn, ptsOut

List1.AddItem "z= " & z

For y = 5 To -5 Step -0.25

Call FindPolyCoeffLH(EqIn, y, z, EqOut, nPoly, Acoeff_0)

ReDim Preserve Acoeff_0(0 To nPoly)

ReDim Preserve ansReal(1 To nPoly)

ReDim Preserve ansImag(1 To nPoly)

Call SolpolyN(nPoly, Acoeff_0, 0.0001, 0, 0, ansReal, ansImag)

For i = 1 To nPoly

If Abs(Round(ansImag(i), 5)) <= 0.0001 Then

xans = Round(ansReal(i), 5)

List1.AddItem "x,y= " & xans & " ; " & y

xp = xans * glAx + y * glAy + z * glAz

yp = xans * glBx + y * glBy + z * glBz

Picture1.FillColor = QBColor(countTL Mod 16)

Picture1.FillStyle = vbSolid

Picture1.Circle (xp, yp), (0.1 + (z) * 0.0125), vbRed 'QBColor(count Mod 16)

ReDim Preserve ptsIn(0 To count)

ptsIn(count).x = Picture2.ScaleWidth \ 2 + CLng(Picture2.ScaleX(xp * 25 - Picture2.ScaleLeft, Picture2.ScaleMode, vbPixels))

ptsIn(count).y = Picture2.ScaleHeight \ 2 + CLng(Picture2.ScaleY(yp * 25 * yFctUse - Picture2.ScaleTop, Picture2.ScaleMode, vbPixels))

stColl.Add Trim(Round(xans, 3) & "," & Round(y, 3) & "," & Round(z, 3))

count = count + 1

End If

Next i

Next y

count = count - 1

If count >= 3 Then

Dim nansHull As Long

nansHull = MakeConvexHull(Picture2, ptsIn, ptsOut, QBColor(count Mod 16))

End If

countTL = countTL + 1

List2.AddItem "*******z= " & z & " ;npt= " & count

Next z

SortNum1_Duplicate stColl

count = 0

For i = 1 To stColl.count

stArray = Split(stColl(i), ",", -1, vbTextCompare)

ReDim Preserve xFun(0 To count), yFun(0 To count), zFun(0 To count)

xFun(count) = Val(stArray(0))

yFun(count) = Val(stArray(1))

zFun(count) = Val(stArray(2))

count = count + 1

Next i

count = count - 1

Dim FileNo As Integer, Fname As String

Fname = "f:\implicitfunction\ImplicitData.dat"

FileNo = FreeFile

Open Fname For Output As #FileNo

For i = 1 To count

Write #FileNo, xFun(i), yFun(i), zFun(i)

Next i

Close #FileNo

Lbltime.Caption = (Timer - time1) & "sec"

End Sub

Sub SolpolyN(Nc As Integer, A() As Double, Tol As Double, Rzero As Double, Szero As Double, ansReal() As Double, ansImag() As Double)

Dim i As Integer

Dim m As Integer, j As Integer, L As Integer, n As Integer, r As Double, S As Double

Dim Radtrm As Double, b(9) As Double, Rc As Double, Sc As Double

Dim p(9) As Double, K As Integer, Rcr As Double, Scr As Double, Q(9) As Double, Rcs As Double

Dim Scs As Double, Denom As Double, Rnum As Double, Snum As Double, Delr As Double, Dels As Double

Dim NewN As Integer, rad As Double, Fa As Double, Fb As Double, Ftpt As Double

'Please note here function :A(0)x^n+A(1)X^(n-1)+A(2)x^(n-2)+........+A(n)

'if 2x^5+3x^4+2x^3+3x^2+4x+5=0 : then A(0)=2,A(1)=3,A(2)=2,A(3)=3,A(4)=4,A(5)=5

'MsgBox ("nc=" & Nc)

On Error Resume Next

For i = 1 To Nc

A(i) = A(i) / A(0)

'MsgBox ("A(I)= " & i & ";" & A(i))

Next i

A(0) = 1

m = 0

j = 1

'!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

r = Rzero 'Rzero initial

S = Szero 'Szero initial

L = 0

n = Nc - 2 * m

' MsgBox ("N=" & n)

Select Case n

'/////////////////////////////////

Case Is < 2

ansReal(j) = -A(1) '

Exit Sub 'GoTo 500

Case Is = 2

'/////////////////////////////////

Fa = A(1) * A(1) - 4# * A(2)

Select Case Fa

Case Is < 0#

'--------------------------------

Radtrm = -(A(1) * A(1) - 4# * A(2))

rad = Sqr(Radtrm)

ansReal(j) = A(1) / 2#

ansReal(j + 1) = -A(1) / 2#

ansImag(j) = rad / 2#

ansImag(j + 1) = -rad / 2#

Exit Sub 'GoTo 500

Case Is = 0#

'--------------------------------------

ansReal(j) = A(1) / 2#

ansReal(j + 1) = -A(1) / 2#

ansImag(j) = 0#

ansImag(j + 1) = 0#

'------------------------

Case Is > 0#

rad = Sqr(A(1) * A(1) - 4# * A(2))

ansReal(j) = (-A(1) + rad) / 2#

ansReal(j + 1) = (-A(1) - rad) / 2#

ansImag(j) = 0#

ansImag(j + 1) = 0#

Exit Sub

End Select

'calculate approx. values of R & S計算R,S近似值

Case Is > 2

End Select

'////////////////////////////////////////////////////

b(1) = A(1) - r

b(2) = A(2) - r * b(1) - S

For K = 3 To n

b(K) = A(K) - r * b(K - 1) - S * b(K - 2)

Next K

Rc = b(n - 1)

Sc = b(n) + r * b(n - 1)

p(1) = -1#

p(2) = r - b(1)

For K = 3 To n

p(K) = -b(K - 1) - r * p(K - 1) - S * p(K - 2)

Next K

Rcr = p(n - 1)

Scr = p(n) + r * p(n - 1) + b(n - 1)

'Calculate b(k) 計算 b(k)偏微分

Q(1) = 0#

Q(2) = -1#

For K = 3 To n

Q(K) = -b(K - 2) - r * Q(K - 1) - S * Q(K - 2)

Next K

Rcs = Q(n - 1)

Scs = Q(n) + r * Q(n - 1)

' modify Denom, Rnum, Snum計算微分修正程式

Denom = Rcr * Scs - Rcs * Scr

Rnum = -Rc * Scs + Sc * Rcs

Snum = -Rcr * Sc + Scr * Rc

Delr = Rnum / Denom

Dels = Snum / Denom

'計算R,S下一階近似值

r = r + Delr

S = S + Dels

'測試微分修正程式是否收斂

If (Abs(Delr) - Tol) <= 0# And (Abs(Dels) - Tol) <= 0# Then Exit Do

'測試迭代次數是否超過預設值

If L > 100 Then Exit Sub

L = L + 1

Loop While True

'計算二次方程式F(M)之一對根值大小

Ftpt = (r * r - 4# * S)

Select Case Ftpt

Case Is < 0#

Radtrm = -Ftpt

rad = Sqr(Radtrm)

ansReal(j) = -r / 2#

ansReal(j + 1) = -r / 2#

ansImag(j) = rad / 2#

ansImag(j + 1) = -rad / 2#

Case Is = 0#

ansReal(j) = -r / 2#

ansReal(j + 1) = -r / 2#

ansImag(j) = 0#

ansImag(j + 1) = 0#

Case Is > 0#

rad = Sqr(Ftpt)

ansReal(j) = (-r + rad) / 2#

ansReal(j + 1) = (-r - rad) / 2#

ansImag(j) = 0#

ansImag(j + 1) = 0#

End Select

'P(N-2)取代P(N)後繼續求解

m = m + 1

j = j + 2

NewN = Nc - 2 * m

For K = 1 To NewN

A(K) = b(K)

Next K

Loop While True

'!!!!!!!!!!!!!!!!!!!!!!!!

End Sub

Please note here the input string of polynomial function should obey the rule of Vb syntax, especially, the power of x, you must use “x^2” not ‘x*x”, but you can

use y*y or y^2 and z*z*z or z^3 for y power or z power. In this article we just talk about how to solve the implicit function not concern about the render of implicit function. If you want to render the implicit function, you need to use some package. The figure(x^2+y^2+z^2-1.0) shown below is using the software program(

marching cube algorithm) wrote by author.

VB_VB NET: chday169

上次修改此網站的日期： 2018年12月02日