
 |

|
|
2013年07月23日 |
上次修改此網站的日期: 2013年07月23日
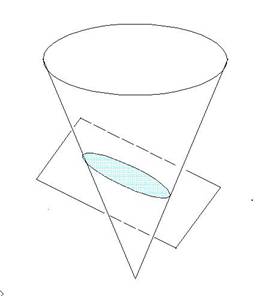
Ellipse is a closed curve of conic section. In other words, an ellipse is a plane curve of an intersection of a cone and a plane. The intersection of cone and a inclined plane will get a ellipse, if the plane is horizontal then the intersection curve is a circle. Ellipses have many similarities with the other two forms of conic sections: the parabolas and the hyperbolas, both of which are open and unbounded.
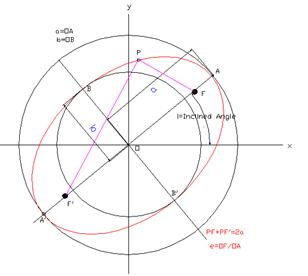
An ellipse is a plane surrounding two focal points such that a straight line drawn from one of the two focal points to any point on the curve and then back to the other focal point on the curve has the same length. As such, it is a generalization of a circle; a circle is a special case of an ellipse that has both focal points at the same point (center). The shape of an ellipse is represented by its eccentricity. The eccentricity of an ellipse can be any number between 0 (a circle) and 1.
Analytically, an ellipse can also be defined as the set of points such that the ratio of the distance of each point on the curve from a given point (called a focus or focal point) to the distance from that same point on the curve to a given line (called the directrix line) is a constant. The value of that constant is the eccentricity of the ellipse. (An eccentricity equal to or greater than one produces the other types of conic sections.)
(a) Drawing of Ellipse
The figure shown below is a general figure of an inclined ellipse with center at (h,k) , a length (a) of semi-mayor axes , a length (b) of semi-minor axes, a inclined angle (i) can be described as:
![]() +
+![]() =1
=1![]() (eq.1)
(eq.1)
If we set
Ta= (a*sin(i))^2+( b*cos(i))^2
Tb= (a*cos(i))^2+( b*sin(i))^2
Tc= 2*sin(i)*cos(i)*(b*b-a*a)
Td= (a*b)^2
Then the general equation of an inclined equation can be rewritten as:
Ta*(x-h)^2+ Tb*(y-k)^2+ Tc* (x-h)*(y-k)= Td (eq.2)
If we define type CadEliipse as
Type CadEllipse
Vertex(0 to 2) as cadpoint ‘or PointF In VB NET
Angle1 as single
Angle2 as single
NuPoint as integer
End Type
If the coordinates of two major axes, myEllipse.Vertex(0) and myEllipse.Vertex(1), and any point, myEllipse.Vertex(2) given ,then we can draw the ellipse by solving the values of b(BB) and i(AngSlop) .
‘ptCen:center of ellipse
ptCen.X = (myEllipse.Vertex(0).X + myEllipse.Vertex(1).X) / 2
ptCen.Y = (myEllipse.Vertex(0).Y + myEllipse.Vertex(1).Y) / 2
Angslop = ATN2((myEllipse.Vertex(1).Y - myEllipse.Vertex(0).Y), (myEllipse.Vertex(1).X - myEllipse.Vertex(0).X)) * Da
AA = Sqr((myEllipse.Vertex(0).X - ptCen.X) ^ 2 + (myEllipse.Vertex(0).Y - ptCen.Y) ^ 2)
ptAny = myEllipse.Vertex(2)
Ta1 = ptAny.X - ptCen.X: Ta2 = AA * Cos(Angslop * Ra): Ta3 = -Sin(Angslop * Ra)
Tb1 = ptAny.Y - ptCen.Y: Tb2 = AA * Sin(Angslop * Ra): Tb3 = Cos(Angslop * Ra)
T1 = (Ta1 * Tb3 - Tb1 * Ta3) / (Ta2 * Tb3 - Ta3 * Tb2)
T2 = (Ta2 * Tb1 - Tb2 * Ta1) / (Ta2 * Tb3 - Ta3 * Tb2)
If (T1 ^ 2 <= 1#) Then Bb = Sqr(T2 ^ 2 / (1 - T1 ^ 2))
The coordinates of any point on ellipse are:
PtAny.x = ptCen.x+AA * Cos(AngI * Ra) * Cos(Angslop * Ra) - BB * Sin(AngI * Ra) * Sin(Angslop * Ra) 'x coordinate
PtAny.y = ptCen.y+AA * Cos(AngI * Ra) * Sin(Angslop * Ra) + BB * Sin(AngI * Ra) * Cos(Angslop * Ra) 'y coordinate
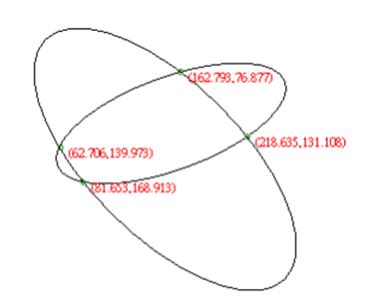
(b)Intersection of two Ellipse
To solve the intersection of two ellipses by hand is quite tedious, but we can solve by computer, the following snippet code is a function of solving the intersection points of two ellipses.
Public Function TwoEllipseIntAll(ByRef myEllipseA As CadEllipse, ByRef myEllipseB As CadEllipse, ByRef ptsInt() As CadPoint, _
ByRef isOnEllipseA() As Boolean, ByRef isOnEllipseB() As Boolean, Optional ByVal xptRefer As Single = -9999#, Optional ByVal yptRefer As Single = -9999#) As Integer
Dim Ae1 As Single, Be1 As Single, h1 As Single, k1 As Single, AngI1 As Single
Dim Ae2 As Single, Be2 As Single, h2 As Single, k2 As Single, AngI2 As Single
Dim Xptin As Single, Yptin As Single
Dim Ta1 As Single, Tb1 As Single, Tc1 As Single, Td1 As Single
Dim Ta2 As Single, Tb2 As Single, Tc2 As Single, Td2 As Single
Dim T1 As Single, T2 As Single, T3 As Single, T4 As Single, T5 As Single, T6 As Single
Dim p1 As Single, p2 As Single, p3 As Single, P4 As Single, P5 As Single, P6 As Single
Dim Atpt As Single, AA(4) As Single, AnsT(4) As Single, AnsV(4) As Single, nans As Integer
Dim q1 As Single, q2 As Single, q3 As Single, Ndat As Integer, i As Integer
Dim Chk1 As Single, Chk2 As Single, Yin1 As Single, Yin2 As Single, AngCita As Single
Dim XtptI As Single, YtptI As Single, Del1 As Single, Del2 As Single, Del3 As Single
Dim XansI(200) As Single, YansI(200) As Single, Smin As Single
Dim A1u As Single, B1u As Single, H1u As Single, K1u As Single, XptU As Single, YptU As Single
Dim A2u As Single, B2u As Single, H2u As Single, K2u As Single, eps As Single, XyFct As Single
Dim Itest As Single, Lmin As Single, Ldel As Single
Dim ptCen As CadPoint, Angslop As Single
Dim Xanst(4), Yanst(4) As Single
TwoEllipseIntAll = -1 'Return
If xptRefer = -9999# And yptRefer = -9999# Then
xptRefer = myEllipseA.pts(0).X
yptRefer = myEllipseA.pts(0).Y
End If
Xptin = xptRefer
Yptin = yptRefer
Call EllipseProp(myEllipseA, ptCen, Ae1, Be1, AngI1)
h1 = ptCen.X
k1 = ptCen.Y
Call EllipseProp(myEllipseB, ptCen, Ae2, Be2, AngI2)
h2 = ptCen.X
k2 = ptCen.Y
ReDim ptsInt(4)
For i = 1 To 4
Xanst(i) = 99999#
Yanst(i) = 99999#
Next i
XyFct = AMAX(Abs(Ae1), Abs(Be1), Abs(Ae2), Abs(Be2))
A1u = Ae1 / XyFct
B1u = Be1 / XyFct
A2u = Ae2 / XyFct
B2u = Be2 / XyFct
H1u = h1 / XyFct
K1u = k1 / XyFct
H2u = h2 / XyFct
K2u = k2 / XyFct
XptU = Xptin / XyFct
YptU = Yptin / XyFct
Ta1 = A1u ^ 2 * Sin(AngI1 * Ra) ^ 2 + B1u ^ 2 * Cos(AngI1 * Ra) ^ 2
Tb1 = A1u ^ 2 * Cos(AngI1 * Ra) ^ 2 + B1u ^ 2 * Sin(AngI1 * Ra) ^ 2
Tc1 = 2 * Sin(AngI1 * Ra) * Cos(AngI1 * Ra) * (B1u ^ 2 - A1u ^ 2)
Td1 = A1u ^ 2 * B1u ^ 2
Ta1 = Ta1 / Td1
Tb1 = Tb1 / Td1
Tc1 = Tc1 / Td1
Td1 = 1#
T1 = -(2# * Ta1 * H1u + Tc1 * K1u)
T2 = -(2# * Tb1 * K1u + Tc1 * H1u)
T3 = Ta1 * H1u ^ 2 + Tb1 * K1u ^ 2 + Tc1 * H1u * K1u - Td1
Ta2 = A2u ^ 2 * Sin(AngI2 * Ra) ^ 2 + B2u ^ 2 * Cos(AngI2 * Ra) ^ 2
Tb2 = A2u ^ 2 * Cos(AngI2 * Ra) ^ 2 + B2u ^ 2 * Sin(AngI2 * Ra) ^ 2
Tc2 = 2 * Sin(AngI2 * Ra) * Cos(AngI2 * Ra) * (B2u ^ 2 - A2u ^ 2)
Td2 = A2u ^ 2 * B2u ^ 2
Ta2 = Ta2 / Td2
Tb2 = Tb2 / Td2
Tc2 = Tc2 / Td2
Td2 = 1#
T4 = -(2# * Ta2 * H2u + Tc2 * K2u)
T5 = -(2# * Tb2 * K2u + Tc2 * H2u)
T6 = Ta2 * H2u ^ 2 + Tb2 * K2u ^ 2 + Tc2 * H2u * K2u - Td2
p1 = Ta1 * T4 - Ta2 * T1
p2 = Ta1 * Tc2 - Ta2 * Tc1
p3 = Tb2 * Tc1 - Tb1 * Tc2
P4 = Tb2 * T1 + Tc1 * T5 - Tb1 * T4 - Tc2 * T2
P5 = T1 * T5 + Tc1 * T6 - T2 * T4 - Tc2 * T3
P6 = T1 * T6 - T3 * T4
q1 = Ta2 * Tb1 - Ta1 * Tb2
q2 = Ta2 * T2 - Ta1 * T5
q3 = Ta2 * T3 - Ta1 * T6
Atpt = q1 ^ 2 - p2 * p3
AA(1) = (2# * q1 * q2 - p1 * p3 - p2 * P4)
AA(2) = (q2 ^ 2 + 2# * q1 * q3 - p1 * P4 - p2 * P5)
AA(3) = (2# * q2 * q3 - p1 * P5 - p2 * P6)
AA(4) = (q3 ^ 2 - p1 * P6)
If Abs(Atpt) < 0.000000000000001 And Abs(AA(1)) < 0.000000000000001 Then
Ndat = 2 '
Atpt = AA(2)
AA(1) = AA(3) / Atpt
AA(2) = AA(4) / Atpt
GoTo 120
End If
If Abs(Atpt) >= 0# Then
Ndat = 4 '
AA(1) = AA(1) / Atpt
AA(2) = AA(2) / Atpt
AA(3) = AA(3) / Atpt
AA(4) = AA(4) / Atpt
End If
120: Yin1 = YptU - 0.05 * AMIN(A1u, A2u, B1u, B2u)
Yin2 = YptU + 0.05 * AMIN(A1u, A2u, B1u, B2u)
eps = 0.01 * AMIN(A1u, A2u, B1u, B2u)
Call SolpolyN(Ndat, AA, eps, Yin1, Yin2, AnsT, AnsV)
nans = 0
For i = 1 To Ndat
If Abs(AnsV(i)) <= 0.000001 Then
nans = nans + 1
Yanst(nans) = AnsT(i)
Xanst(nans) = (q1 * Yanst(nans) ^ 2 + q2 * Yanst(nans) + q3) / (p1 + p2 * Yanst(nans))
End If
Next i
If nans = 0 Then
MsgBox ("no solution 無合理解")
Exit Function
End If
Chk1 = (Ta1 * (Xanst(1) - H1u) ^ 2 + Tb1 * (Yanst(1) - K1u) ^ 2 + Tc1 * (Xanst(1) - H1u) * (Yanst(1) - K1u) - Td1) / Td1
Chk2 = (Ta2 * (Xanst(1) - H2u) ^ 2 + Tb2 * (Yanst(1) - K2u) ^ 2 + Tc2 * (Xanst(1) - H2u) * (Yanst(1) - K2u) - Td2) / Td2
'Lmin = 99999.0#
If nans >= 1 Then
For i = 1 To nans
Xanst(i) = Xanst(i) * XyFct
Yanst(i) = Yanst(i) * XyFct
Next i
End If
Dim count As Integer: count = 0
For i = 1 To nans
ReDim Preserve ptsInt(count), isOnEllipseA(count), isOnEllipseB(count)
ptsInt(count).X = CSng(Xanst(i))
ptsInt(count).Y = CSng(Yanst(i))
isOnEllipseA(count) = IsPtOnEllArcCurve_byPoint(myEllipseA, ptsInt(count))
isOnEllipseB(count) = IsPtOnEllArcCurve_byPoint(myEllipseB, ptsInt(count))
count = count + 1
Next
500:
If UBound(ptsInt) >= 0 Then TwoEllipseIntAll = UBound(ptsInt) 'return
End Function
Because an ellipse can be considered as a collection of line segments which all points are on the ellipse, we can use the method of intersection of two lines to get same result. Please note the maximum number of intersection points is 4,the minimum are 0.If we use two line intersection method ,then don’t forget to remove the duplicate point(s).The intersection of line and ellipse, or the intersection of line and ellipse ,or ellipse and arc can be solved by the same way. If we convert a ellipse to circle,then the method of two ellipse intersection method can be used to solve the intersection of ellipse and circle.
Private Function LineLineIntReal(LineA As cadLine, LineB As cadLine, iPoints() As CadPoint) As Integer
Dim Xa1 As Single, Ya1 As Single, Xa2 As Single, Ya2 As Single
Dim Xb1 As Single, Yb1 As Single, Xb2 As Single, Yb2 As Single
Dim aX As Single, aY As Single, Bx As Single, By As Single
Dim T1 As Single, T2 As Single
Dim cx As Single, cy As Single, dx As Single, dy As Single
Dim tpt As Single, tpt1 As Single, tpt2 As Single, i As Integer
Erase iPoints()
On Error Resume Next
Xa1 = LineA.pts(0).X
Ya1 = LineA.pts(0).Y
Xa2 = LineA.pts(1).X
Ya2 = LineA.pts(1).Y
Xb1 = LineB.pts(0).X
Yb1 = LineB.pts(0).Y
Xb2 = LineB.pts(1).X
Yb2 = LineB.pts(1).Y
aX = Xa2 - Xa1
aY = Ya2 - Ya1
Bx = Xb1 - Xb2
By = Yb1 - Yb2
cx = Xa1 - Xb1
cy = Ya1 - Yb1
tpt = aY * Bx - aX * By
tpt1 = By * cx - Bx * cy
T1 = tpt1 / tpt
tpt2 = aX * cy - aY * cx
T2 = tpt2 / tpt
If (T1 >= -0.0001 And T1 <= 1.0001) And (T2 >= -0.0001 And T2 <= 1.0001) Then
ReDim Preserve iPoints(0)
iPoints(0).X = Xa1 + T1 * (Xa2 - Xa1)
iPoints(0).Y = Ya1 + T1 * (Ya2 - Ya1)
LineLineIntReal = 0
Exit Function
End If
LineLineIntReal = -1
End Function
(c) Tangent line of two Ellipse
From any point outside a ellipse can draw a two lines to tangent the ellipse.
The following snippet code is a function to find two tangent points to a ellipse.
Function Ellipse2Tans(ByRef myPtGiven As CadPoint, ByRef myEllipse As CadEllipse, ByRef pttans() As CadPoint) As Integer
Ellipse2Tans = -1
Dim Fa As Single, Fb As Single, Fc As Single, tpt As Single
Dim Ta As Single, Tb As Single, Tc As Single, Td As Single
Dim Te As Single, Tf As Single
Dim T1 As Double, T2 As Double, T3 As Double, T4 As Double, T5 As Double, T6 As Double, T7 As Double
Dim ptAns1 As CadPoint, ptAns2 As CadPoint
Dim ptCen As CadPoint, AA As Single, Bb As Single, Angslop As Single
Call EllipseProp(myEllipse, ptCen, AA, Bb, Angslop)
ptAns1.X = 99999#
ptAns1.Y = 99999#
ptAns2.X = 99999#
ptAns2.Y = 99999#
Ta = AA ^ 2 * Sin(Angslop * Ra) ^ 2 + Bb ^ 2 * Cos(Angslop * Ra) ^ 2
Tb = AA ^ 2 * Cos(Angslop * Ra) ^ 2 + Bb ^ 2 * Sin(Angslop * Ra) ^ 2
Tc = 2 * Sin(Angslop * Ra) * Cos(Angslop * Ra) * (Bb ^ 2 - AA ^ 2)
Td = AA ^ 2 * Bb ^ 2
Te = ptCen.X - myPtGiven.X
Tf = ptCen.Y - myPtGiven.Y
T1 = 2# * Ta * Te + Tc * Tf
T2 = Tc * Te + 2# * Tb * Tf
T3 = -(Tb * T1 - Tc * T2) / Ta / T1
T4 = 2 * Tc * Td / Ta / T1
T5 = Td / Ta
T6 = -T2 / T1
T7 = -2# * Td / T1
Fa = T6 ^ 2 - T3
Fb = 2 * T6 * T7 - T4
Fc = T7 ^ 2 - T5
tpt = Fb ^ 2 - 4# * Fa * Fc
If tpt <= 0# Then
MsgBox ("no solution for Ellipse Tangent line")
Ellipse2Tans = -1
Exit Function
End If
ptAns1.Y = (-Fb - Sqr(tpt)) / 2# / Fa
ptAns2.Y = (-Fb + Sqr(tpt)) / 2# / Fa
ptAns1.X = T6 * ptAns1.Y + T7
ptAns2.X = T6 * ptAns2.Y + T7
ptAns1.X = ptAns1.X + ptCen.X '平移
ptAns1.Y = ptAns1.Y + ptCen.Y '平移
ptAns2.X = ptAns2.X + ptCen.X
ptAns2.Y = ptAns2.Y + ptCen.Y
ReDim Preserve pttans(0 To 1) ', Ltans(0 To 1)
pttans(0).X = ptAns1.X
pttans(0).Y = ptAns1.Y
pttans(1).X = ptAns2.X
pttans(1).Y = ptAns2.Y
Ellipse2Tans = 1
' Ltans(0) = Sqr((PtTans(0).X - myPtGiven.X) ^ 2 + (PtTans(0).Y - myPtGiven.Y) ^ 2)
'Ltans(1) = Sqr((PtTans(1).X - myPtGiven.X) ^ 2 + (PtTans(1).Y - myPtGiven.Y) ^ 2)
End Function

