
|
|
土壤強度圓弧破壞模式偏微分回算分析
10.1
前言
第九章所提及之”已破壞邊坡之剪力強度回算分析(Back
determination of the shear strength parameters in failed slopes)”,主要內容是在利用數學之偏微分公式,以單一破壞邊坡斷面資料,直接推導回算出已破壞土壤之剪力強度。該文為土壤剪力強度回算計算之學術報告,因此部份微積分公式必須補實後,方能應適用在實際工程作業中,下面我們要討論是如何補實及實際應用。
10.2
土壤圓弧破壞剪力強度回算分析
10.2.1
坡趾下破壞模式
如圖10.2.1.1圓弧破壞土壤強度回算分析,係將公式(9.1)中之F(i,j,θ)假定為1,求解c 與 與 之方式。 之方式。
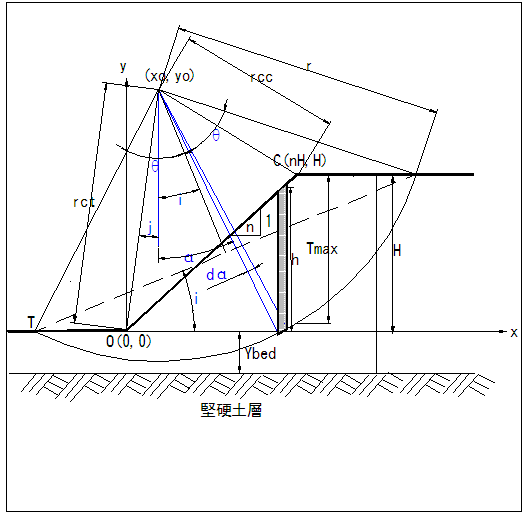
圖10.2.1.1
破壞圓弧示意圖

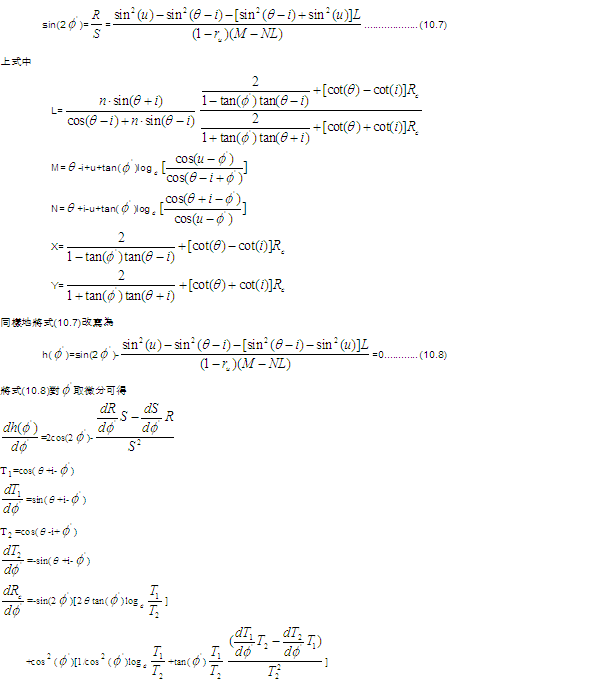
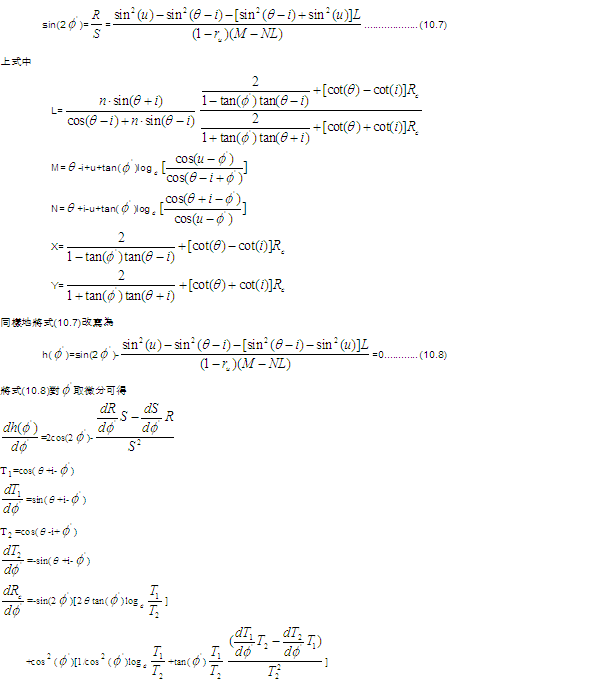

【例題10.1】
中國陜西省距離西安市火車站東方約1公里附近之某工地,於1970年開挖施工完工,至1981年9月間雨季後第一次發現邊坡壁面產生鼓脹變形,同年11月20日突然坍方。破壞現址土壤屬紅棕色沉泥質粘土,破壞面為相當平滑之圓弧如圖E10.1.1所示,依據Zao
and Han(1984)所作之試驗室之試驗,其殘餘強度:c =50Kpa, =50Kpa,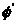 =11°,據此所推算出之Bishop修正法安全係數為1.19,試推算土壤之強度?(題目取材自He報告p666) =11°,據此所推算出之Bishop修正法安全係數為1.19,試推算土壤之強度?(題目取材自He報告p666)
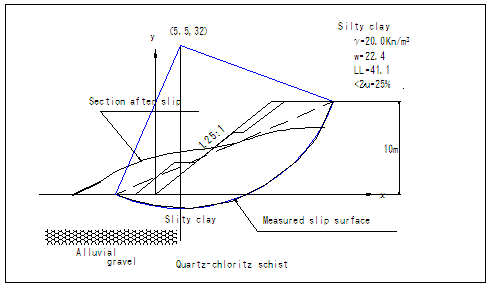
圖E10.1.1
地層斷面示意圖
【Excel解法】
(1)
經調查在未發生坍方前之邊坡地形為不規則坡面,為方便分析,特將原坡面地表改以等面積之單一斜坡取代,其坡度約為1.25:1(水平比垂直),地下水水壓比(Pore
pressure ratio,r ),估計約為0.1。圖E10.1.2為破壞弧之詳細圖示。 ),估計約為0.1。圖E10.1.2為破壞弧之詳細圖示。
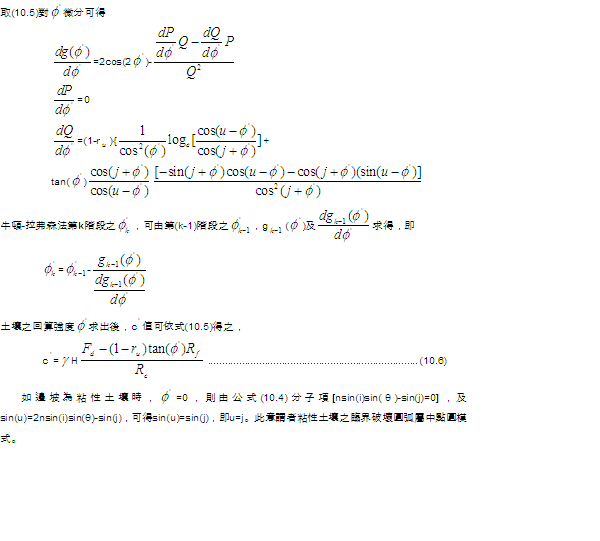
(2) 利用公式(10.5),以牛頓-拉弗森數值解法,可求得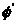 為11.2658°,及利用公式(10.6)
求得c 為11.2658°,及利用公式(10.6)
求得c 為3.1219
t/㎡。相關Excel
試算結果如表E10.1.1所示。 為3.1219
t/㎡。相關Excel
試算結果如表E10.1.1所示。
(3)
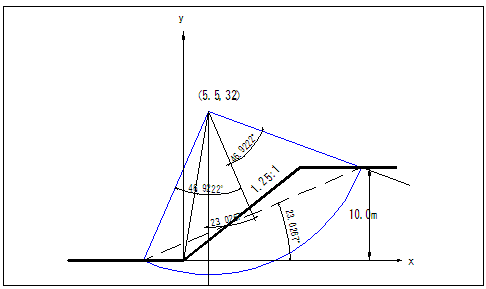
圖E10.1.3為利用「圓弧滑動偏微分強度回算法」電腦程式分析結果及圖示。
(4) 原He報告則為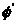 =11.868°,c =11.868°,c =31.111Kpa(3.172t/㎡),兩者相當吻合。 =31.111Kpa(3.172t/㎡),兩者相當吻合。
圖E10.1.2 破壞弧斷面圖
表E10.1.1
Excel試算表
|
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
1 |
?uww |
?uws |
?ru |
?Hslp |
?Slpn |
?xctr |
?yctr |
?rad. |
|
|
|
|
2 |
1 |
2.0394 |
0 |
20 |
1.25 |
5.500
|
32.000 |
35 |
|
|
|
|
3 |
?eps1 |
da |
ra |
|
|
|
|
|
|
|
|
|
4 |
0.001 |
57.2958 |
0.01745 |
|
|
|
|
|
|
|
|
|
5 |
xctr |
yctr |
rad. |
adcpi |
adcmi |
adc |
adi |
adj |
adu |
ade |
|
|
6 |
5.5000 |
32.0000 |
35.0000 |
69.9490 |
23.8955 |
46.9222 |
23.0267 |
9.0411 |
33.8584 |
31.5127 |
|
|
7 |
agri |
agrj |
agrc |
agru |
agre |
|
|
|
|
|
|
|
8 |
0.4019
|
0.1578
|
0.8189
|
0.5909
|
0.5500
|
|
|
|
|
|
|
|
9 |
k=1 |
phi1-1 |
dPdp |
dQdp |
P |
tp1 |
Q |
dgdp |
f(phi) |
phi-2 |
phians(deg) |
|
10 |
|
0.0000
|
0.0000
|
-0.1733
|
0.2857
|
0.8409
|
0.7487
|
1.9117
|
-0.3816
|
0.1996
|
9999.0000
|
|
11 |
k=2 |
phi1-1 |
dPdp |
dQdp |
P |
tp1 |
Q |
dgdp |
f(phi) |
phi-2 |
phians(deg) |
|
12 |
|
0.1996
|
0.0000
|
0.1312
|
0.2857
|
0.9868
|
0.7460
|
1.9101
|
0.0057
|
0.1966
|
9999.0000
|
|
13 |
k=3 |
phi1-1 |
dPdp |
dQdp |
P |
tp1 |
Q |
dgdp |
|
phi-2 |
phians(deg) |
|
14 |
|
0.1966
|
0.0000
|
0.1267
|
0.2857
|
0.9844
|
0.7456
|
1.9125
|
0.0000
|
0.1966
|
11.2658
|
|
15 |
k=4 |
phi1-1 |
dPdp |
dQdp |
P |
tp1 |
Q |
dgdp |
f(phi) |
phi-2 |
phians(deg) |
|
16 |
|
0.1966
|
0.0000
|
0.1267
|
0.2857
|
0.9844
|
0.7456
|
1.9125
|
0.0000
|
0.1966
|
11.2658
|
|
17 |
k=5 |
phi1-1 |
dPdp |
dQdp |
P |
tp1 |
Q |
dgdp |
f(phi) |
phi-2 |
phians(deg) |
|
18 |
|
0.1966
|
0.0000
|
0.1267
|
0.2857
|
0.9844
|
0.7456
|
1.9125
|
0.0000
|
0.1966
|
11.2658
|
|
19 |
k=6 |
phi1-1 |
dPdp |
dQdp |
P |
tp1 |
Q |
dgdp |
f(phi) |
phi-2 |
phians(deg) |
|
20 |
|
0.1966
|
0.0000
|
0.1267
|
0.2857
|
0.9844
|
0.7456
|
1.9125
|
0.0000
|
0.1966 |
11.2658 |
|
21 |
agri |
agrj |
agrc |
agru |
agre |
|
|
|
check? |
|
|
|
22 |
0.4019
|
0.1578
|
0.8189
|
0.5909
|
0.5500
|
|
|
|
sin(2*phir) |
P/Q |
|
|
23 |
tpa |
tpb |
tpc |
tpd |
tpe |
Fd |
Rc |
ff1 |
0.3832
|
0.3832
|
|
|
24 |
0.6358
|
6.8768
|
0.5630
|
2.1534
|
0.9844
|
0.2476
|
1.4886
|
-2.3818
|
|
|
|
|
25 |
ff2 |
ff3a |
ff3b |
ff3c |
Rf |
c' |
check Fs? |
|
|
|
|
|
26 |
0.4958
|
1.2805
|
0.1467
|
0.1149
|
0.6709
|
3.1219 |
1.0000
|
|
|
|
|
|
|
A |
B |
C |
D |
|
17 |
k=5 |
phi1-1 |
dPdp |
dQdp |
|
18 |
|
=J16 |
0 |
=(1-ru)*(1/COS(B18)^2
*LN((COS(D$8-B18)
/COS(B$8+B18))
+TAN(B18)
*COS(B$8+B18)
/COS($E16-B18)
*(SIN(D$8-B18)
*COS(B$8+B18)
+COS(D$8-B18)
*SIN(B$8+B18))
/COS(B$8+B18)^2)) |
|
19 |
k=6 |
phi1-1 |
dPdp |
dQdp |
|
20 |
|
=J18 |
0 |
=(1-ru)*(1/COS(B20)^2
*LN((COS(D$8-B20)
/COS(B$8+B20))
+TAN(B20)
*COS(B$8+B20)
/COS($E18-B20)
*(SIN(D$8-B20)
*COS(B$8+B20)
+COS(D$8-B20)
*SIN(B$8+B20))
/COS(B$8+B20)^2)) |
|
21 |
agri |
agrj |
agrc |
agru |
|
22 |
=A8 |
=B8 |
=C8 |
=IF(ABS(2*Slpn
*SIN(A22
*SIN(C22)-SIN(B22))
>1,9999,ASIN(2*Slpn
*SIN(A22)
*SIN(C22)
-SIN(B22))) |
|
23 |
tpa |
tpb |
tpc |
tpd |
|
24 |
=COS(C22+A22-J20)
/COS(C22-A22+J20) |
=TAN(45*ra+0.5
*(C22+A22-J20))
/TAN(45*ra-0.5
*(C22-A22+J20)) |
=COS(C22+A22-J20)
/COS(D22-J20) |
=TAN(45*ra
+0.5*(D22-J20))
/TAN(45*ra-0.5
*(B22+J20)) |
|
25 |
ff2 |
ff3a |
ff3b |
ff3c |
|
26 |
=IF(C24<0,9999,COS(J20)^2
*(C22+A22-D22+TAN(J20)
*LN(C24))) |
=IF(B24>0,2*SIN(C22)
*COS(A22+J20)
+SIN(J20)^2
*LN(B24),9999) |
=IF(D24<0,9999,
COS(B22-J20)
-COS(D22+J20)
-0.5*SIN(2*J20)
*LN(D24)) |
=IF(E24<0,9999,
SIN(B22)
*COS(J20)
*(D22+B22
+TAN(J20)
*LN(E24))) |
|
|
E |
F |
G |
|
17 |
|
tp1 |
Q |
|
18 |
=4*Slpn*SIN(A$8)*SIN(C$8)
*(Slpn*SIN(A$8)*SIN(C$8)
-SIN(B$8)) |
=COS(D$8-B18)
/COS(B$8+B18) |
=(1-ru)*(D$8+B$8
+TAN(B18)*LN(F18)) |
|
19 |
P |
tp1 |
Q |
|
20 |
=4*Slpn*SIN(A$8)*SIN(C$8)
*(Slpn*SIN(A$8)*SIN(C$8)
-SIN(B$8)) |
=COS(D$8-B20)
/COS(B$8+B20) |
=(1-ru)*(D$8+B$8
+TAN(B20)*LN(F20)) |
|
21 |
agre |
|
|
|
22 |
=SIN(B22)/SIN(A22)
/SIN(C22) |
|
|
|
23 |
tpe |
Fd |
Rc |
|
24 |
=COS(D22-J20)
/COS(B22+J20) |
=1/3*(SIN(A22)
*SIN(C22))^2
*(1-2*Slpn^2+3*E22
*(Slpn-0.5*E22)
+1.5*(1/TAN(A22)^2
+1/TAN(C22)^2)) |
=IF(A24>0,COS(J20)^2
*(2*C22+TAN(J20)
*LN(A24)),9999) |
|
25 |
Rf |
c' |
check Fs? |
|
26 |
=H24+A26+(B26
+(C26+D26)/Slpn)
*COS(J20)/2/SIN(A22)
/SIN(C22) |
=uws*Hslp*(F24-(1-ru)
*TAN(J20)*E26)/G24 |
=(F26/uws/Hslp*G24
+(1-ru)*TAN(J20)
*E26)/F24 |
|
|
H |
I |
J |
K |
|
17 |
dgdp |
f(phi) |
phi-2 |
phians(deg) |
|
18 |
=2*COS(2*B18)-(C18*G18
-D18*E18)/G18^2 |
=SIN(2*B18)-E18/G18 |
=B18-I18/H18 |
=IF(ABS(J18-B18)
<=eps1,J18*da,9999) |
|
19 |
dgdp |
f(phi) |
phi-2 |
phians(deg) |
|
20 |
=2*COS(2*B20)-(C20*G20
-D20*E20)/G20^2 |
=SIN(2*B20)-E20/G20 |
=B20-I20/H20 |
=IF(ABS(J20-B20)
<=eps1,J20*da,9999) |
|
21 |
|
check? |
|
|
|
22 |
|
sin(2*phir) |
P/Q |
|
|
23 |
ff1 |
=SIN(2*J20) |
=E20/G20 |
|
|
24 |
=-0.5*(1+1/TAN(A22)
/TAN(C22))*G24 |
|
phi-2 |
phians(deg) |
|
25 |
|
|
=B18-I18/H18 |
=IF(ABS(J18-B18)
<=eps1,J18*da,9999) |
|
26 |
|
|
phi-2 |
phians(deg) |
圖E10.1.3
「圓弧滑動偏微分強度回算法」電腦程式分析結果及圖示
【例題10.2】
發生於中國陜西省巴都河瀏陽(Badu
river,Leuyang,譯音)附近之河谷邊坡,於1979年2月15日發生坍方,根據1979年現場鑽探調查資料,推測其破壞圓弧約如圖E10.2.1所示,地下水水壓比估計為0。另依據試驗室力學試驗結果:已破壞土壤尖峰強度(Post-peak
strength)為 =15°,c =15°,c =13Kpa。利用Bishop修正法公式計算,其安全係數僅達0.79,很明顯地,試驗結果並無法合理解釋破壞原因?試分析推算土壤之強度?(題目取材自He報告p666) =13Kpa。利用Bishop修正法公式計算,其安全係數僅達0.79,很明顯地,試驗結果並無法合理解釋破壞原因?試分析推算土壤之強度?(題目取材自He報告p666)
【Excel解法】
(1)
觀察圖E10.2.2破壞弧之詳細圖示,破壞弧圓心為(-19,238)時,其與坡底直線交點有(-38,0)與(0,0)兩處。
(2)
如取破壞弧通過(-38,0)及坡趾(0,0),依牛頓-拉弗森數值解法,可得c =2.5177 =2.5177
t/㎡,及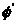 =17.2598°。相關Excel試算部份結果如表E10.2.1所示。 =17.2598°。相關Excel試算部份結果如表E10.2.1所示。
(3)
如取破壞弧不通過(-38,0)僅通過坡趾(0,0),可求得c =1.3122t/㎡, =1.3122t/㎡,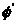 =
21.7808°。相關Excel試算部份結果如表E10.2.2所示。 =
21.7808°。相關Excel試算部份結果如表E10.2.2所示。
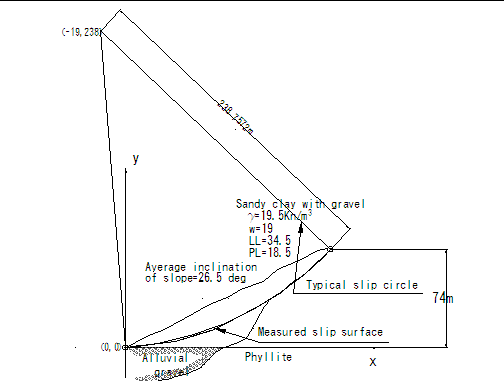
 圖E10.2.1
地層斷面示意圖 圖E10.2.1
地層斷面示意圖

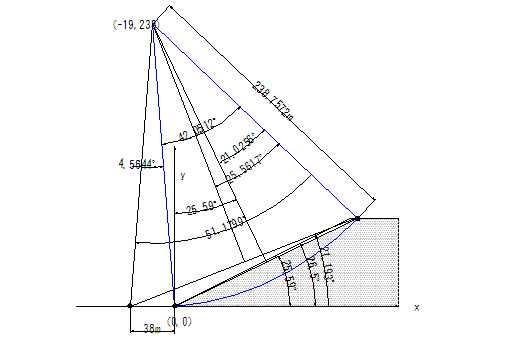
圖E10.2.2
破壞弧斷面圖
表E10.2.1
Excel 試算表
|
?uww |
?uws |
?ru |
?Hslp |
?Slpn |
?xctr |
?yctr |
|
|
|
|
|
1 |
1.9884 |
0.0000 |
74.0000 |
2.0057 |
-19.0000 |
238.0000 |
|
|
|
|
|
?eps1 |
da |
ra |
|
|
|
|
|
|
|
|
|
0.001 |
57.29578 |
0.017453 |
|
|
|
|
|
|
|
|
|
xctr |
yctr |
rad. |
adcpi |
adcmi |
adc |
adi |
adj |
|
|
|
|
-19.0000
|
238.0000
|
238.7572
|
46.6156
|
4.5644 |
25.5900
|
21.0256
|
-4.5644
|
|
|
|
|
agri |
agrj |
agrc |
agru |
agre |
|
|
|
|
|
|
|
0.3670
|
-0.0797
|
0.4466
|
0.7771
|
-0.5135
|
|
|
|
|
|
|
|
k=5 |
phi1-1 |
Rc |
X |
Y |
M |
N |
L |
dmdf |
TA |
TB |
|
|
0.3012
|
0.7968
|
1.6417
|
5.2419
|
0.8433
|
0.0304
|
0.3948
|
1.0000
|
0.8716
|
0.9284
|
|
|
dTAdf |
dTBdf |
dRcdf |
dXdf |
dYdf |
dLdf |
dMdf |
dNdf |
|
|
|
|
0.4903
|
-0.3717
|
-0.2853
|
0.3306
|
-2.6525
|
0.2793
|
0.3796
|
-0.0069
|
|
|
|
|
dRdf |
dSdf |
R(phi) |
S(phi) |
h(phi) |
dhdf |
phi-2 |
phians(deg) |
|
|
|
|
-0.0102
|
0.3739
|
0.4710
|
0.8313
|
0.0000
|
1.9151
|
0.3012
|
17.2558
|
|
|
|
k=6 |
phi1-1 |
Rc |
X |
Y |
M |
N |
L |
dmdf |
TA |
TB |
|
|
0.3012
|
0.7968
|
1.6417
|
5.2419
|
0.8433
|
0.0304
|
0.3948
|
1.0000
|
0.8716
|
0.9284
|
|
|
dTAdf |
dTBdf |
dRcdf |
dXdf |
dYdf |
dLdf |
dMdf |
dNdf |
|
|
|
|
0.4903
|
-0.3717
|
-0.2853
|
0.3306
|
-2.6525
|
0.2793
|
0.3796
|
-0.0069
|
|
|
|
|
dRdf |
dSdf |
R(phi) |
S(phi) |
h(phi) |
dhdf |
phi-2 |
phians(deg) |
|
|
|
|
-0.0102
|
0.3739
|
0.4710
|
0.8313
|
0.0000
|
1.9151
|
0.3012
|
17.2558 |
|
|
|
|
agri |
agrj |
agrc |
agru |
agre |
|
|
sin(2*phir) |
|
|
|
|
0.3670
|
-0.0797
|
0.4466
|
0.7771
|
-0.5135
|
|
|
0.5666
|
|
|
|
|
tpa |
tpb |
tpc |
tpd |
tpe |
Fd |
Rc |
R/S |
|
|
|
|
0.9388
|
2.5265
|
0.9805
|
2.0510
|
0.9111
|
0.0493
|
0.7968
|
0.5666
|
|
|
|
|
ff1 |
ff2 |
ff3a |
ff3b |
ff3c |
Rf |
c' |
check Fs? |
|
|
|
|
-2.5626
|
0.0277
|
0.7597
|
0.2520
|
-0.0508
|
0.1149
|
2.5177 |
1.0000
|
|
|
表E10.2.2
Excel試算表
|
?uww |
?uws |
?ru |
?Hslp |
?Slpn |
?xctr |
?yctr |
|
|
|
|
|
1 |
1.9884 |
0.0000 |
74.0000 |
2.0057 |
-19.0000 |
238.0000 |
|
|
|
|
|
?eps1 |
da |
ra |
|
|
|
|
|
|
|
|
|
0.001 |
57.29578 |
0.017453 |
|
|
|
|
|
|
|
|
|
xctr |
yctr |
rad. |
adcpi |
adcmi |
adc |
adi |
adj |
|
chk adj? |
|
|
-19.0000
|
238.0000
|
238.7572
|
46.6156
|
-4.5644 |
21.0256
|
25.5900
|
-4.5644
|
|
-4.5644
|
|
|
agri |
agrj |
agrc |
agru |
agre |
|
|
|
|
|
|
|
0.4466
|
-0.0797
|
0.3670
|
0.7771
|
-0.5135
|
|
|
|
|
|
|
|
k=1 |
phi1-1 |
Rc |
X |
Y |
M |
N |
L |
dmdf |
TA |
TB |
|
|
0.0000
|
0.7339
|
2.3769
|
5.4419
|
0.6974
|
0.0365
|
0.7605
|
1.0000
|
0.6869
|
0.9968
|
|
|
dTAdf |
dTBdf |
dRcdf |
dXdf |
dYdf |
dLdf |
dMdf |
dNdf |
|
|
|
|
0.7268
|
0.0796
|
-0.3724
|
-0.3509
|
-3.8626
|
0.4275
|
-0.3352
|
-0.0372
|
|
|
|
|
dRdf |
dSdf |
R(phi) |
S(phi) |
h(phi) |
dhdf |
phi-2 |
phians(deg) |
|
|
|
|
-0.0156
|
-0.3225
|
0.4576
|
0.6697
|
-0.6834
|
1.6942
|
0.4033
|
9999.0000
|
|
|
|
k=2 |
phi1-1 |
Rc |
X |
Y |
M |
N |
L |
dmdf |
TA |
TB |
|
|
0.4033
|
0.6088
|
2.2468
|
4.2332
|
0.6897
|
0.0301
|
0.9241
|
1.0000
|
0.9170
|
0.9481
|
|
|
dTAdf |
dTBdf |
dRcdf |
dXdf |
dYdf |
dLdf |
dMdf |
dNdf |
|
|
|
|
0.3988
|
-0.3181
|
-0.2748
|
-0.3176
|
-2.4761
|
0.4099
|
0.4846
|
0.0004
|
|
|
|
|
dRdf |
dSdf |
R(phi) |
S(phi) |
h(phi) |
dhdf |
phi-2 |
phians(deg) |
|
|
|
|
-0.0149
|
0.4719
|
0.4517
|
0.6619
|
0.0396
|
1.8929
|
0.3824
|
9999.0000
|
|
|
|
k=3 |
phi1-1 |
Rc |
X |
Y |
M |
N |
L |
dmdf |
TA |
TB |
|
|
0.3824
|
0.6146
|
2.2534
|
4.2853
|
0.6840
|
0.0301
|
0.9155
|
1.0000
|
0.9085
|
0.9545
|
|
|
dTAdf |
dTBdf |
dRcdf |
dXdf |
dYdf |
dLdf |
dMdf |
dNdf |
|
|
|
|
0.4179
|
-0.2981
|
-0.2764
|
-0.3161
|
-2.5062
|
0.4070
|
0.4279
|
-0.0011
|
|
|
|
|
dRdf |
dSdf |
R(phi) |
S(phi) |
h(phi) |
dhdf |
phi-2 |
phians(deg) |
|
|
|
|
-0.0148
|
0.4167
|
0.4520
|
0.6565
|
0.0039
|
1.9026
|
0.3804
|
9999.0000
|
|
|
|
k=4 |
phi1-1 |
Rc |
X |
Y |
M |
N |
L |
dmdf |
TA |
TB |
|
|
0.3804
|
0.6152
|
2.2540
|
4.2905
|
0.6835
|
0.0301
|
0.9147
|
1.0000
|
0.9076
|
0.9551
|
|
|
dTAdf |
dTBdf |
dRcdf |
dXdf |
dYdf |
dLdf |
dMdf |
dNdf |
|
|
|
|
0.4198
|
-0.2962
|
-0.2766
|
-0.3160
|
-2.5093
|
0.4067
|
0.4225
|
-0.0012
|
|
|
|
|
dRdf |
dSdf |
R(phi) |
S(phi) |
h(phi) |
dhdf |
phi-2 |
phians(deg) |
|
|
|
|
-0.0148
|
0.4114
|
0.4520
|
0.6560
|
0.0004
|
1.9035
|
0.3802
|
21.7819
|
|
|
|
k=5 |
phi1-1 |
Rc |
X |
Y |
M |
N |
L |
dmdf |
TA |
TB |
|
|
0.3802
|
0.6152
|
2.2541
|
4.2910
|
0.6834
|
0.0301
|
0.9146
|
1.0000
|
0.9075
|
0.9552
|
|
|
dTAdf |
dTBdf |
dRcdf |
dXdf |
dYdf |
dLdf |
dMdf |
dNdf |
|
|
|
|
0.4200
|
-0.2960
|
-0.2766
|
-0.3159
|
-2.5096
|
0.4067
|
0.4220
|
-0.0012
|
|
|
|
|
dRdf |
dSdf |
R(phi) |
S(phi) |
h(phi) |
dhdf |
phi-2 |
phians(deg) |
|
|
|
|
-0.0148
|
0.4109
|
0.4520
|
0.6559
|
0.0000
|
1.9036
|
0.3801
|
21.7808
|
|
|
|
k=6 |
phi1-1 |
Rc |
X |
Y |
M |
N |
L |
dmdf |
TA |
TB |
|
|
0.3801
|
0.6152
|
2.2541
|
4.2910
|
0.6834
|
0.0301
|
0.9146
|
1.0000
|
0.9075
|
0.9552
|
|
|
dTAdf |
dTBdf |
dRcdf |
dXdf |
dYdf |
dLdf |
dMdf |
dNdf |
|
|
|
|
0.4200
|
-0.2960
|
-0.2766
|
-0.3159
|
-2.5096
|
0.4067
|
0.4220
|
-0.0012
|
|
|
|
|
dRdf |
dSdf |
R(phi) |
S(phi) |
h(phi) |
dhdf |
phi-2 |
phians(deg) |
|
|
|
|
-0.0148
|
0.4109
|
0.4520
|
0.6559
|
0.0000
|
1.9036
|
0.3801
|
21.7807 |
|
|
|
|
agri |
agrj |
agrc |
agru |
agre |
|
|
sin(2*phir) |
|
|
|
|
0.4466
|
-0.0797
|
0.3670
|
0.7771
|
-0.5135
|
|
|
0.6891
|
|
|
|
|
tpa |
tpb |
tpc |
tpd |
tpe |
Fd |
Rc |
R/S |
|
|
|
|
0.9501
|
2.1229
|
0.9840
|
2.0399
|
0.9655
|
0.0493
|
0.6152
|
0.6891
|
|
|
|
|
ff1 |
ff2 |
ff3a |
ff3b |
ff3c |
Rf |
c' |
check Fs? |
|
|
|
|
-1.9788
|
0.0259
|
0.5896
|
0.2486
|
-0.0505
|
0.1097
|
1.3122 |
1.0000
|
|
|
(4) He報告c =13.463Kpa(1.373t/㎡), =13.463Kpa(1.373t/㎡), =21.697°,與(2)兩者答案尚稱吻合。 =21.697°,與(2)兩者答案尚稱吻合。
(5)
利用CFDay.Exe以Bishop修正法計算,採用c =1.373t/㎡, =1.373t/㎡, =21.697°,切片範圍為(0,0)至(154.519,74)時,則安全係數為1.0414,切片範圍為(-38,0)至(154.519,74)時為1.0416;如c =21.697°,切片範圍為(0,0)至(154.519,74)時,則安全係數為1.0414,切片範圍為(-38,0)至(154.519,74)時為1.0416;如c =2.5177t/㎡, =2.5177t/㎡,
 =17.2588°,切片範圍為(0,0)至(154.519,74)時則安全係數為0.9951,切片範圍為(-38,0)至(154.519,74)時為0.9949。 =17.2588°,切片範圍為(0,0)至(154.519,74)時則安全係數為0.9951,切片範圍為(-38,0)至(154.519,74)時為0.9949。
(6)
表E10.2.3及圖E10.2.4為c =2.5177t/㎡, =2.5177t/㎡, =17.2588°,圓心(-19,238)固定,半徑與安全係數之關係變化關係圖。 =17.2588°,圓心(-19,238)固定,半徑與安全係數之關係變化關係圖。
(7)
圖E10.2.5為利用「圓弧滑動偏微分強度回算法」電腦程式分析結果及圖示。
(8)
由步驟(5)及步驟(6)顯示坡趾破壞模式切片範圍(0,0)~(154.519,74)與(-38,0)~(154.519,74)變化對整體安全係數之影響相當有限,因此為使坡趾破壞模式與坡趾下破壞模式,兩者在破壞弧接近或通過坡趾時符合數學極限及函數連續之觀念,編者較傾向採用c =2.5177t/㎡, =2.5177t/㎡, =17.2588°,唯在實際之邊坡設計時,基於安全考量,建議宜採用兩組答案中之較保守之c =17.2588°,唯在實際之邊坡設計時,基於安全考量,建議宜採用兩組答案中之較保守之c , , 值。 值。
表E10.2.3
圓心(-19,238)固定半徑vs安全係數
|
Xcen |
Ycen |
Rad. |
Fdr. |
Fs(ORD.) |
Fs(BSP.) |
|
-19 |
-238 |
255 |
3986.4 |
1.293 |
1.4096 |
|
-19 |
-238 |
250 |
3312.2 |
1.209 |
1.3023 |
|
-19 |
-238 |
248 |
3040.9 |
1.174 |
1.2576 |
|
-19 |
-238 |
246 |
2763.5 |
1.138 |
1.2124 |
|
-19 |
-238 |
244 |
2489.6 |
1.101 |
1.1656 |
|
-19 |
-238 |
242 |
2213.4 |
1.065 |
1.1193 |
|
-19 |
-238 |
240 |
1933.2 |
1.028 |
1.0712 |
|
-19 |
-238 |
239 |
1793.9 |
1.009 |
1.047 |
|
-19 |
-238 |
238.758 |
1760 |
1.005 |
1.0417 |
|
-19 |
-238 |
238.757 |
1755.9 |
1.005 |
1.0414 |
|
-19 |
-238 |
238.756 |
1755.9 |
1.005 |
1.0412 |
|
-19 |
-238 |
237 |
1512.7 |
0.975 |
1.0017 |
|
-19 |
-238 |
235 |
1243.4 |
0.99 |
1.014 |
|
-19 |
-238 |
233 |
982.3 |
1.016 |
1.0362 |
|
-19 |
-238 |
231 |
742.2 |
1.052 |
1.0684 |
|
-19 |
-238 |
229 |
523.9 |
1.109 |
1.122 |
|
-19 |
-238 |
225 |
172.6 |
1.421 |
1.4267 |
 
圖E10.2.4
圓心(-19,238)固定,半徑與安全係數變化關係圖

圖E10.2.5
「圓弧滑動偏微分強度回算法」電腦程式分析結果及圖示
|

