
|
|

|
|
2019年03月24日 |
上次修改此網站的日期: 2018年12月02日
等密度圖製作
0. 前言
傳統上人工繪製π圖,係利用等面積投影網,將岩層不連續面位態之極點(Pole)資料投影至網上成為極點圖(Point diagram)。有了極點圖後,再利用適當方法計算極點的分佈密度百分比,並進一步繪製成等密度圖(Countoured diagram)。計算極點密度百分比之方法甚多,以下只介紹較常用者:(1)細胞網狀計數法(Cell counting method),(2)格子點法(Grid or Schimidt method),及(3)美利斯法(Mellis method)等三種。三種方法都利用投影網百分之一面積為計數網圖,在投影面上或球體上計數各不同位置資料點的出現頻率,並換算成百分比密度。
1. 丹尼斯曲線細胞網狀計數法(Deness Curvilinear cell counting method)
丹尼斯曲線細胞計數法,主要係利用丹尼斯所繪製之計數網圖(詳圖1.1及表1.1),以計數落在計數網圖各細胞格內之資料點數之謂。圖1.1(a)適用在傾角較陡峭接近垂直之不連續面;而圖1.1(b)則較常用在一般之傾斜不連續面資料。圖1.2為利用丹尼斯計數網圖計數法之圖示,網格內之數字為資料點數。
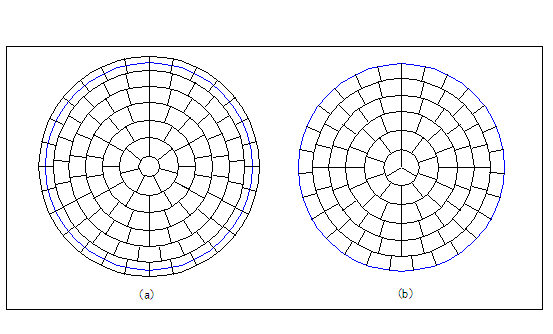
圖1.1丹尼斯曲線細胞網圖
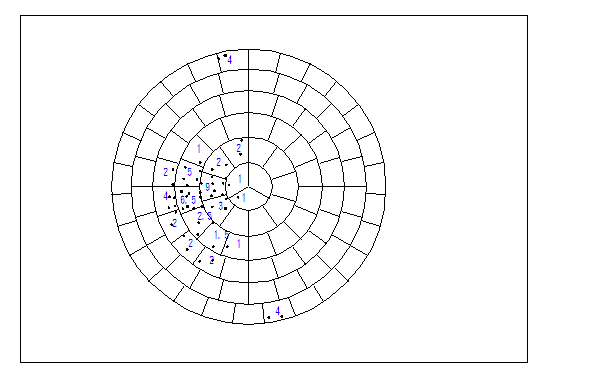
圖1.2丹尼斯細胞網計數資料圖
表1.1細胞網狀尺寸資料表示
|
丹尼斯A式 |
丹尼斯B式 |
同心圓 |
||||||
|
細胞數 |
淨半徑 |
角度 |
細胞數 |
淨半徑 |
角度 |
細胞數 |
淨半徑 |
傾角 |
|
1 |
0.100 |
360.0000 |
3 |
0.172 |
120.0000 |
10 |
0.3162 |
25.8419 |
|
7 |
0.283 |
51.4285 |
10 |
0.360 |
36.0000 |
10 |
0.4472 |
36.8699 |
|
12 |
0.447 |
30.0000 |
16 |
0.539 |
22.5000 |
10 |
0.5477 |
45.5730 |
|
18 |
0.616 |
20.0000 |
20 |
0.700 |
18.0000 |
10 |
0.6325 |
53.1301 |
|
22 |
0.775 |
16.3636 |
24 |
0.855 |
15.0000 |
10 |
0.7071 |
60.0000 |
|
25 |
0.923 |
14.4000 |
27 |
1.000 |
13.3333 |
10 |
0.7746 |
66.4218 |
|
28 |
1.064 |
12.8571 |
|
|
|
10 |
0.8367 |
72.5424 |
|
|
|
|
|
|
|
10 |
0.8944 |
78.4630 |
|
|
|
|
|
|
|
10 |
0.9487 |
84.2608 |
|
|
|
|
|
|
|
10 |
1.0000 |
90.0000 |
2. 同心圓細胞網狀計數法(Concentric cell counting method)
同心圓細胞網格圖如圖2.1及表2.1所示者,圖2.2為利用同心圓
細胞網格之計數結果。
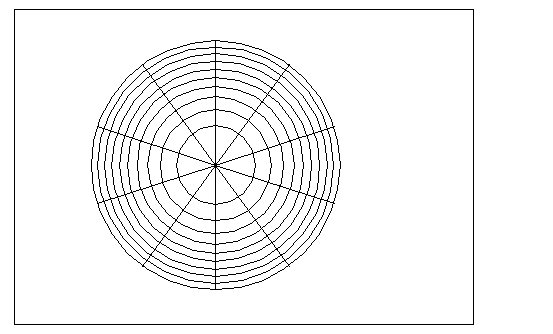
圖2.1同心圓細胞網圖
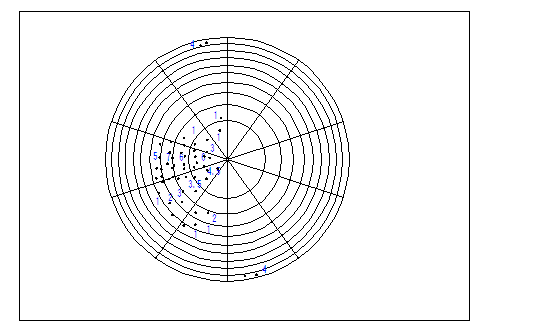
圖4.2同心圓細胞網狀計數資料圖
3. 格子點法(Grid or Schimidt method)
格子點法為將計數圓之圓心置放於預先安排好之格子點(21×21或41×41,詳如圖3.1)上,然後計算落在計數圓內之資料點數(如圖3.2下方鄰近基圓圓心之計數圓,資料點數為5),再轉換成百分比值,接近圓周之資料點可利用丹尼斯計數雙圓(Counting circles,圖3.2下方之圖示)計數,其資料數為丹尼斯計數雙圓內之資料點總額數。一般人工繪製等密度圖多採用此法,圖3.3即為人工繪製之等密度圖。
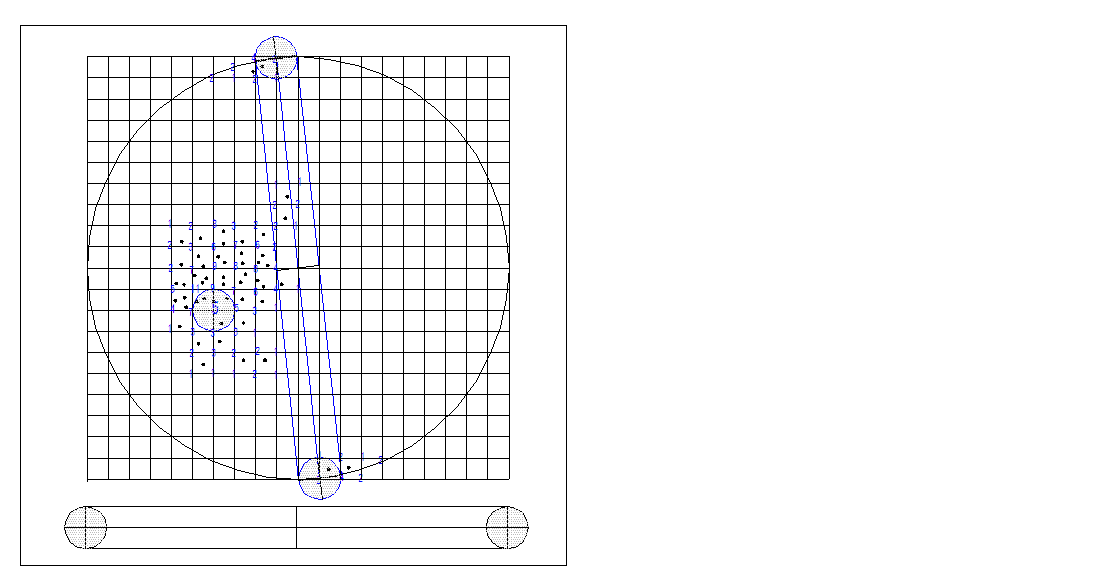
圖3.1格子點計數資料圖
 圖3.2格子點計數法人工繪製等密度圖
圖3.2格子點計數法人工繪製等密度圖
4. 美利斯法(Mellis method )

計數圓內時,可檢驗其夾角是否大於8°6’34”,或PG是否大於R。
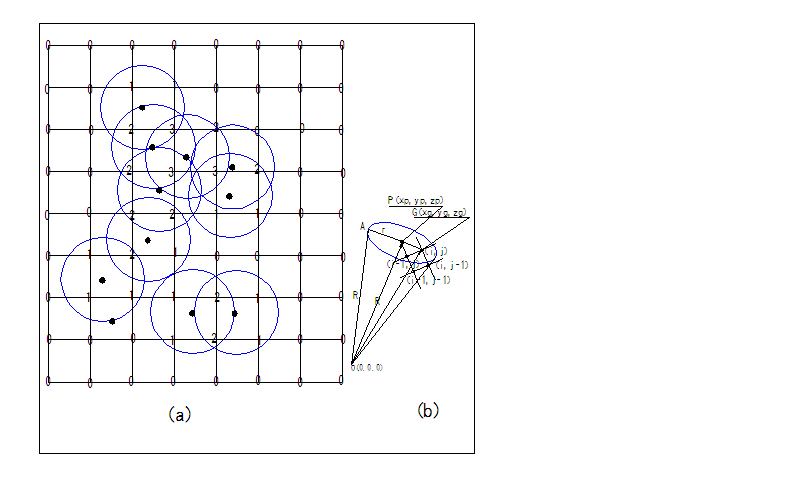
圖4.1資料點計數法
5.等密度圖電腦繪圖簡介
人工計數方法,不但費時費力並極易出錯外,因其計數工作係在投影面上進行,等面積投影網所使用之計數圓雖然能保持等面積,但卻無法保持等角度,為計數工作主要誤差來源。利用電腦繪製π圖時,一般多以等面積投影網法,或美利斯法設計電腦程式。在設計程式時兩種方法都使用計數網格,所不同的是等面積投影網法將計數圓放在網格交點上,計數落在圓內的資料點數;而美利斯法,則將計數圓置於資料點上,計算計數圓內所涵蓋之網格點數。無論使用等面積投影網法或美利斯法,基本上計算結果是應該相同的,但後者較為節省尋點時間,故較常採用。
早期電腦程式多以人工在投影面上做計數工作,因此精確度較差。亞德勒等人(Adler and others,1968)及瓦那(Warner,1969)等,首先在渠等所設計之程式,率先採用在球面上計數之方法。卡爾卡尼與凡夫里斯(Kalkani and Von Frese,1976及1979)及柯貝克與西德傑(Kohlbeck and Scheidegger,1977)等之研究論述又分別強調及證明在球面上計數的優越及必要性。因此在球面上計數己成為近年來此方面電腦程式的新趨勢,在國內陳修齊與陳隆煇(1980)、李錫堤(1984)等學者專家,亦多已採用此計數法。在等密度圖方面,早期的電腦程式多只做到計數到密度值,等密度線尚須以人工繪製,近年來此方面的電腦程式,則多已能自動繪製等密度圖[Kalkani and von Frese(1980),葉勇凱(Yeh,1984)及李錫堤(1984),Ling-Yun,Chiao(1985)等。其中喬凌雲及李錫堤等已嘗試以P.C個人電腦繪製等密度線;葉勇凱則嘗試自動計算集中眼中心點之座標。上述各家之程式多有其優劣點,有興趣之讀者可閱讀附錄所列之參考資料。前面所介紹之電腦解法,多以福傳語言編纂,必須配合繪圖機製圖。本書所附之電腦程式有關等密度圖部份,主要係參考Chiao(1985)發表之『Fortran-v program for contouring point density on pi-diagrams using a microcomputer』以Visual Basic 6語言編纂者。資料格子密度分佈數值圖、極點圖、β圖及π圖均可先在視窗上繪製完成,校核無誤後再以Bmp圖檔存放在User指定目錄下。表5.1為台北市南港路麗山里節理資料(莊明勇,1983),圖5.1為利用電腦程式『等密度圖繪製』所繪製之極點圖,圖5.5.2為利用『等密度圖繪製』繪製之資料格子密度分佈數值圖(0~10,A(11),B(12)……),圖5.3為利用『等密度圖繪製』繪製之β圖,圖5.4為利用『等密度圖繪製』繪製之等密度圖,圖5.5為利用筆者所編製之3D等密度圖程式所繪製『等密度圖』。
表5.1台北市南港路麗山里節理資料(莊明勇,1983)
|
N80.0E |
83.0W |
N75.0E |
72.0W |
N14.0W |
77.0E |
N16.0W |
76.0E |
|
N07.0W |
79.0E |
N72.0E |
71.0W |
N78.0E |
78.0W |
N12.0W |
82.0E |
|
N75.0E |
70.0W |
N20.0W |
75.0E |
N18.0W |
75.0E |
N70.0E |
81.0W |
|
N70.0E |
78.0W |
N07.0W |
76.0E |
N85.0W |
75.0E |
N72.0E |
82.0W |
|
N80.0E |
82.0W |
N86.0W |
66.0E |
N70.0E |
71.0W |
N74.0E |
72.0W |
|
N36.0W |
80.0W |
N63.0W |
76.0E |
N78.0W |
87.0W |
N35.0W |
62.0E |
|
N56.0W |
68.0W |
N06.0W |
59.0W |
N90.0E |
73.0W |
N15.0W |
76.0W |
|
N90.0E |
81.0E |
N62.0E |
78.0W |
N80.0E |
80.0W |
N02.0W |
82.0W |
|
N01.0E |
78.0W |
N09.0W |
85.0E |
N36.0W |
68.0W |
N33.0W |
90.0E |
|
N55.0E |
54.0W |
N41.0W |
72.0E |
N08.0W |
90.0E |
N82.0E |
78.0W |
|
N10.0W |
74.0E |
N70.0E |
73.0W |
N00.0E |
69.0W |
N71.0E |
73.0W |
|
N30.0E |
78.0W |
N68.0E |
71.0W |
N77.0E |
74.0W |
N72.0E |
73.0W |
|
N60.0W |
50.0W |
N77.0E |
85.0W |
N58.0W |
90.0E |
N56.0W |
68.0W |
|
N49.0W |
67.0E |
N15.0W |
84.0E |
N81.0E |
78.0E |
N90.0E |
83.0W |
|
N84.0E |
82.0W |
N72.0W |
78.0E |
N86.0W |
68.0E |
N90.0E |
69.0E |
|
N03.0E |
78.0W |
N83.0W |
76.0W |
N63.0W |
90.0W |
N64.0W |
90.0E |
|
N24.0W |
80.0W |
N81.0E |
80.0W |
N78.0E |
60.0W |
N36.0E |
70.0W |
|
N22.0E |
57.0W |
N03.0W |
74.0W |
N80.0W |
72.0E |
N12.0W |
83.0W |
|
N13.0W |
82.0W |
N33.0W |
86.0W |
N61.0W |
90.0E |
N45.0W |
74.0W |
|
N14.0W |
83.0W |
N68.0W |
90.0E |
N83.0W |
72.0E |
N22.0W |
60.0E |
|
N80.0E |
83.0W |
N48.0E |
20.0E |
N84.0W |
85.0E |
N63.0E |
71.0W |
|
N13.0W |
77.0E |
N78.0E |
85.0W |
N80.0E |
90.0E |
N81.0E |
87.0W |
|
N70.0W |
72.0E |
N13.0W |
83.0W |
N08.0W |
85.0W |
N39.0E |
21.0E |
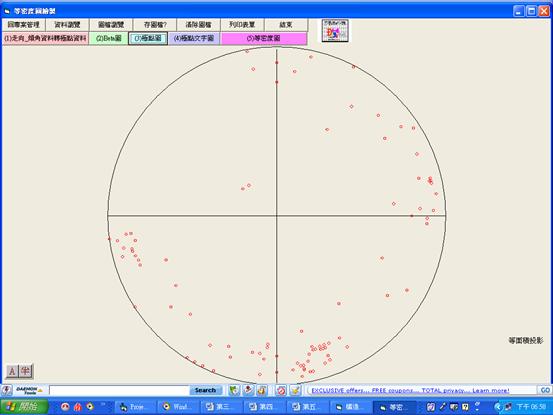
圖5.1電腦程式『等密度圖繪製』南港路麗山里節理極點圖成果畫面
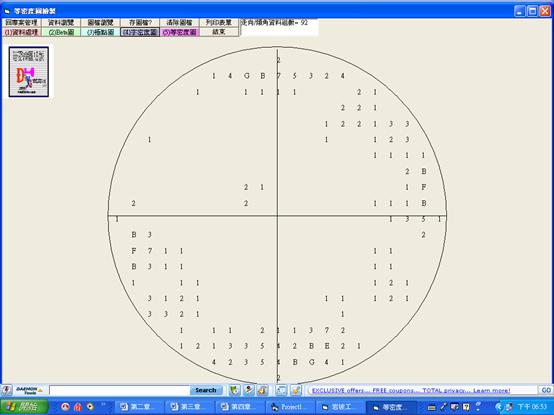
圖5.2電腦程式『等密度圖繪製』資料格子密度分佈數值圖成果畫面
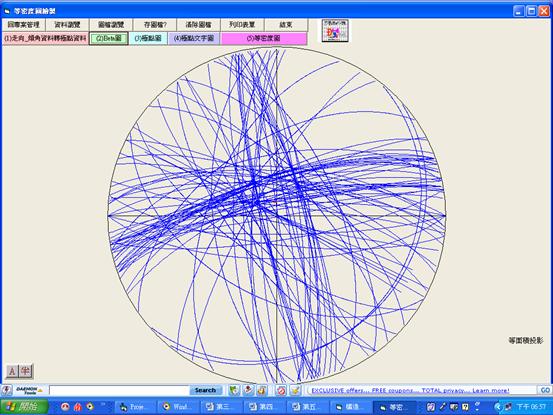
圖5.3電腦程式『等密度圖繪製』南港路麗山里節理β圖成果畫面
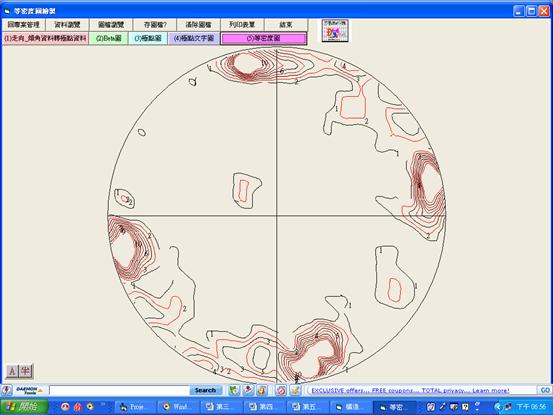
圖5.4電腦程式『等密度圖繪製』南港路麗山里等密度圖成果畫面
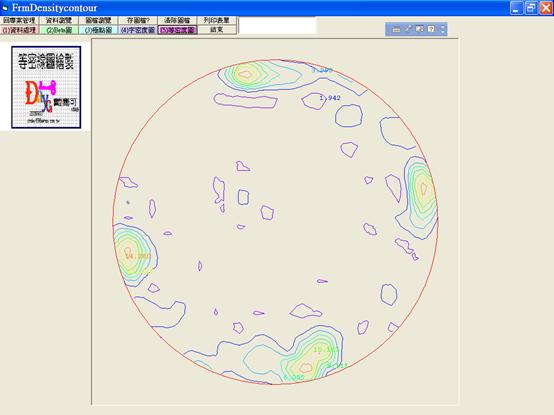
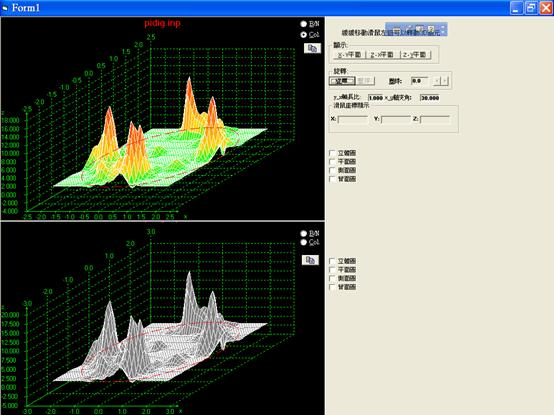
圖5.5『等密度圖』南港路麗山里等密度圖成果畫面