
|
|

|
|
2019年03月24日 |
|
|
 |
|
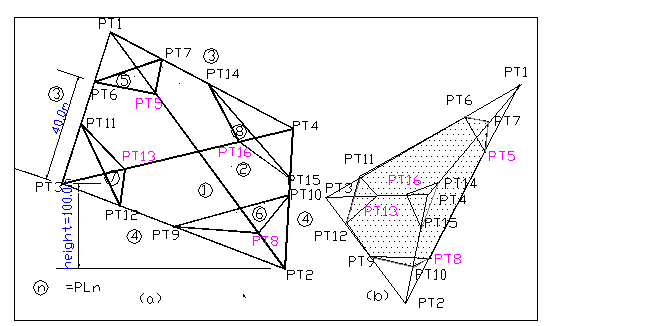
Wedge failure by Excel spreadsheet
Limit equilibrium analysis of rock wedge failure by vector method and system equations method have been discussed “in Wedge failure of rock slope”, the algorithm by using Excel Spreadsheet discuss here is quite similar as the computer methods by vector method and system equations method. In this paper the definition of rock wedge geometry use the system equation method, also. The number of discontinuity plane in Excel spreadsheet method can be up to eight by default, The basic wedge is cut by plane 1(PL1) to PL4 ,PL5 to PL8 are tension crack planes. Every two tension crack plane can not overlapped, it means that every two tension crack planes do not having line intersection within basic wedge. The plunge of earth quake (EQ) can be assumed as horizontal or in the worst condition to get the minimum safety factor. The plunge of rock bolt can be assumed any direction or along the most economic plunge with the less bolt force.
[Example 1]:
A rock wedge cut by 4 discontinuities and a tension crack plane):
PL 1(left bottom) 2(right bottom) 3(Up.) 4(Low.) 5(tension crack)
Dip d.(°) 105 235 195 185 165
Dip(°) 45 70 12 65 70
c![]() =0.5k/ft
=0.5k/ft![]() ,
c
,
c![]() =1.0k/ft
=1.0k/ft![]() ,
,![]()
![]() =20
=20![]() ,
,![]()
![]() =30
=30![]() ,
,![]() =0.160k/ft
=0.160k/ft![]() ,
,![]() =0.0625k/ft
=0.0625k/ft![]()
![]() =100ft,
=100ft,![]() -
-![]() =40ft。computing(1)
Fs of no ground water,(2)Fs with ground water,(3)f=FS of EQ without ground water,(4)Fs
of E=8000k.
=40ft。computing(1)
Fs of no ground water,(2)Fs with ground water,(3)f=FS of EQ without ground water,(4)Fs
of E=8000k.
The minimum safety factor in normal condition is 1.5,while he minimum safety factor in during EQ is 1.3 (Hoek & Bray 1977).
[Sol]:
The number of discontinuity is 8 by default. If indplane =1 then represent this plane is existing, otherwise this plane is non- existing. The height of line 4(L4) is 100.00 ft, i.e Lzg_4=100.00. On tension crack plane 5, the length for point 6 to point 3 is 40.0ft(L(X-B)). If tension crack 5(PL5) is not existing, then the PT5, PT6, PT7 all shrink to PT1, if tension crack 6(PL6) is not existing, then the PT8, PT9, PT10 all shrink to PT2,…….
(1) Data input:
|
item |
data name |
description |
|
1 |
?uww |
Unit weight of water(t/m^3 or kip/ft^3) |
|
2 |
?uwr |
Unit weight of rock wedge |
|
3 |
?cs1?~?cs2 |
Cohesion of plane 1 & plane 2 |
|
4 |
?ph1?~?ph2 |
friction angle of plane 1 & plane 2 |
|
5 |
?Ce |
horizontal acceleration of EQ |
|
6 |
?Fsn |
minimum safety factor without EQ |
|
7 |
?Fse |
minimum safety factor with EQ |
|
8 |
?Plane_no |
no. of discontinuity plane of wedge |
|
9 |
?ind_bot? |
Index of horizontal angle of bolt:ind_bot=0 for most economic, ind_bot<>0, then input,horizontal angle of bolt |
|
10 |
?did |
dip direction of discontinuity plane |
|
11 |
?dip |
dip angle of discontinuity plane |
|
12 |
?indplane |
Index of plane,ndplane=1 for has this plane, indplane=0 no this plane |
|
13 |
?Lg |
length of wedge line segment, if unknown set it to 0 |
|
14 |
?Lxg |
x component of wedge line segment, if unknown set it to 0 |
|
15 |
?Lyg |
y component of wedge line segment, if unknown set it to 0 |
|
16 |
?Lzg |
z component of wedge line segment, if unknown set it to 0 |
|
17 |
?L(A_X) |
length of line on tension crack from vertex to nearest point, if unknown set it to 0 |
|
18 |
?L(B_X) |
length of line on tension crack from vertex to farest point, if unknown set it to 0 |
|
19 |
?hwtpn |
Water of point n ,n=6,11,12,9,8,7,14,15,10 etc. |
(2) Definition of variables name in spread sheet:
|
item |
variabls |
description |
|
1 |
abotgdid |
dip direction of rock bolt |
|
2 |
abotgdip |
dip angle of rock bolt |
|
3 |
csh1~csh2 |
cohesion on PL1 and PL2 |
|
4 |
dac |
180/pi() |
|
5 |
Eqf |
coeff. of EQ |
|
6 |
Fctgw |
Factor of water force(0 or 1) |
|
7 |
Fdnoeq1 |
driving force(excluding EQ force) in EQ worst condition |
|
8 |
Fdnoeq2 |
driving force(excluding EQ force) along intersected line |
|
9 |
Frnoeq1 |
resisting force(excluding EQ force) in EQ worst condition |
|
10 |
Frnoeq2 |
resisting force(excluding EQ force) along intersected line |
|
11 |
Fse |
minimum Fs during EQ |
|
12 |
Fsn |
minimum Fs without EQ |
|
13 |
hwpt1~hwpt16 |
water head for point 1~16 |
|
14 |
indbot |
index of horizontal angle of bolt |
|
15 |
L1f~L6f |
final length of line1~6 |
|
16 |
L6tpt |
length of line 6 while d=10 of PL4 |
|
17 |
L1use~L5use |
actual length of line1~5 |
|
18 |
Mx1~Mx3 |
z component of vector M for sliding case1~3 |
|
19 |
Mxe1~Mxe3 |
x component of vector M for sliding case1~3 during EQ |
|
20 |
My1~My3 |
y component of vector M for sliding case1~3 |
|
21 |
Mye1~Mye3 |
z component of vector M for sliding case1~3 during EQ |
|
22 |
Mz1~Mz3 |
z component of vector M for sliding case1~3 |
|
23 |
Mze1~Mze3 |
z component of vector M for sliding case1~3 during EQ |
|
24 |
n1dotr2 |
dot product of unit normal vector n1& n2 |
|
25 |
n2dotr1 |
dot product of unit normal vector n2 & unit position vector r1 |
|
25 |
phi~ph2 |
friction angle on PL1 & PL2 |
|
26 |
planeno |
total number of discontinuity plane |
|
27 |
Px1~Px3 |
x component of virtual vector P for sliding case1~3 |
|
28 |
Py1~Py3 |
y component of virtual vector P for sliding case1~3 |
|
29 |
Pz1~Py3 |
z component of virtual vector P for sliding case1~3 |
|
30 |
Qx1~Qx3 |
x component of virtual vector Q for sliding case1~3 |
|
31 |
Qy1~Qy3 |
y component of virtual vector Q for sliding case1~3 |
|
31 |
Qz1~Qy3 |
z component of virtual vector Q for sliding case1~3 |
|
32 |
rac |
Pi()/180 |
|
33 |
St1~St3 |
sum of cohesion force for sliding cas 1 ~3 |
|
34 |
uix1~uix6 |
x component of unit vector of line segment 1~6 |
|
35 |
uiy1~uiy6 |
y component of unit vector of line segment 1~6 |
|
36 |
uiz1~uiz6 |
z component of unit vector of line segment 1~6 |
|
37 |
und1~und8 |
d value of ax+by+cz=d for plane 1~8 |
|
38 |
unx1~unx8 |
x component of unit normal for plane 1~8 |
|
39 |
uny1~uny8 |
y component of unit normal for plane 1~8 |
|
40 |
unz1~unz8 |
z component of unit normal for plane 1~8 |
|
41 |
uix1,uiy1,uiz1 |
x,y,z component of unit vector of intersected line of PL1 & PL2 |
|
42 |
uwr |
Unit weight of rock |
|
43 |
uww |
Unit weight of water |
|
44 |
(ux1,uy1,uz1) |
x,y,z component of unit vector of position vector of PL1 |
|
45 |
(ux2,uy2,uz2) |
x,y,z component of unit vector of position vector of PL2 |
|
46 |
(xsl1,ysl1,zsl1) |
x,y,z component of unit vector along sliding line for sliding case 1 |
|
47 |
(xsl2,ysl2,zsl2) |
x,y,z component of unit vector along sliding line for sliding case 2 |
|
48 |
(xsl3,ysl1,zsl3) |
x,y,z component of unit vector along sliding line for sliding case 3 |
|
49 |
xpt1~xpt16 |
x coord. of point 1~ 6 |
|
50 |
ypt1~ypt16 |
y coord. of point 1~ 6 |
|
51 |
zpt1~zpt16 |
z coord. of point 1~ 6 |

Figure E1.1 Wedge diagram
Table E1.1 Data input
|
|
ind-bot<>0 for input bolt did/dip |
|
|
|
|
|
|
|
|
||
|
|
?uww |
?uwr |
?cs1 |
?phi1 |
?cs2 |
?phi2 |
?Ce |
?Fsn |
?Fse |
?plane_no |
?ind-bolt |
|
|
|||||||||||
|
vector |
?did |
?dip |
vector |
?indplane |
?did |
?dip |
|
|
|
||
|
1 |
1 |
105.00 |
45.00 |
5 |
165.0 |
70.00 |
|
|
|||
|
2 |
1 |
235.00 |
70.00 |
6 |
180.0 |
75.00 |
|
|
|
||
|
3 |
1 |
195.00 |
13.00 |
|
7 |
230.0 |
85.00 |
|
|
||
|
4 |
1 |
185.00 |
65.00 |
|
8 |
100.0 |
73.00 |
|
|
|
|
Table E1.1 Data input(continue)
|
|
|
Lg |
Lxg |
Lyg |
Lzg |
|
|
|
|
|
|
|
|
1 |
0.00 |
0.00 |
0.00 |
0.00 |
|
|
|
|
|
|
|
|
2 |
0.00 |
0.00 |
0.00 |
0.00 |
|
|
|
|
|
|
|
|
3 |
0.00 |
0.00 |
0.00 |
0.00 |
|
|
|
|
|
|
|
|
4 |
0.00 |
0.00 |
0.00 |
100.00 |
|
|
|
|
|
|
|
|
5 |
0.00 |
0.00 |
0.00 |
0.00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pl5 |
|
|
|
近端至中間點 |
遠端至中間點 |
pl6 |
|
|
|
|
|
|
Line |
PtA(near) |
PtX(mid) |
PtB(far) |
?L(A-X) |
?L(X-B) |
Line |
PtA(near) |
PtX(mid) |
PtB(far) |
?L(A-X) |
?L(X-B) |
|
L1' |
1 |
5 |
2 |
0.00 |
0.00 |
L1'' |
2 |
8 |
1 |
00.00 |
0.00 |
|
L2' |
1 |
6 |
3 |
0.00 |
40.00 |
L4" |
2 |
9 |
3 |
0.00 |
0.00 |
|
L3' |
1 |
7 |
4 |
0.00 |
0.00 |
L5' |
2 |
10 |
4 |
0.00 |
0.00 |
(3)Cood. Of wedge vertices:
To compute vertices of rock wedge, e assume d=-10 , then modify by the ratio of given length and computed length. From PT1,PT3 we can compute PT6.Because triangle PT5,6,7 is a closed polygon, then we can compute PT6 and PT7 by vector operation.
表E1.2 Cood. Of baseic wedge
|
pt1 |
a |
b |
c |
d |
b |
c |
a |
d |
c |
a |
b |
d |
|
|
|
pl1 |
0.1830 |
-0.6830 |
0.7071 |
0.0000 |
-0.6830 |
0.7071 |
0.1830 |
0.0000 |
0.7071 |
0.1830 |
-0.6830 |
0.0000 |
x |
0.0000 |
|
pl2 |
0.5390 |
0.7698 |
0.3420 |
0.0000 |
0.7698 |
0.3420 |
0.5390 |
0.0000 |
0.3420 |
0.5390 |
0.7698 |
0.0000 |
y |
0.0000 |
|
pl3 |
0.2008 |
0.0538 |
0.0000 |
0.0538 |
0.9781 |
0.2008 |
0.0000 |
0.9781 |
0.2008 |
0.0538 |
0.0000 |
z |
0.0000 |
|
|
pt2 |
a |
b |
c |
d |
b |
c |
a |
d |
c |
a |
b |
d |
|
|
|
pl1 |
0.1830 |
-0.6830 |
0.00 |
-0.6830 |
0.7071 |
0.1830 |
0.0000 |
0.7071 |
0.1830 |
-0.6830 |
0.0000 |
x |
-16.8356 |
|
|
pl2 |
0.5390 |
0.7698 |
0.00 |
0.7698 |
0.3420 |
0.5390 |
0.0000 |
0.3420 |
0.5390 |
0.7698 |
0.0000 |
y |
6.8936 |
|
|
pl4 |
0.9029 |
0.0790 |
-10.00 |
0.0790 |
0.4226 |
0.9029 |
-10.0000 |
0.4226 |
0.9029 |
0.0790 |
-10.0000 |
z |
11.0161 |
|
|
pt3 |
a |
b |
c |
d |
b |
c |
a |
d |
c |
a |
b |
d |
|
|
|
pl1 |
0.00 |
-0.6830 |
0.7071 |
0.1830 |
0.0000 |
0.7071 |
0.1830 |
-0.6830 |
0.0000 |
x |
-1099 |
|||
|
pl3 |
0.00 |
0.0538 |
0.9781 |
0.2008 |
0.0000 |
0.9781 |
0.2008 |
0.0538 |
0.0000 |
y |
-0.6399 |
|||
|
pl4 |
-10.00 |
0.0790 |
0.4226 |
0.9029 |
-10.0000 |
0.4226 |
0.9029 |
0.0790 |
-10.0000 |
z |
2.5421 |
|||
|
pt4 |
a |
b |
c |
d |
b |
c |
a |
d |
c |
a |
b |
d |
|
|
|
0.5390 |
0.3420 |
0.00 |
0.7698 |
0.3420 |
0.5390 |
0.0000 |
0.3420 |
0.5390 |
0.7698 |
0.0000 |
x |
-13.7993 |
||
|
0.2008 |
0.9781 |
0.00 |
0.0538 |
0.9781 |
0.2008 |
0.0000 |
0.9781 |
0.2008 |
0.0538 |
0.0000 |
y |
7.9898 |
||
|
0.9029 |
0.4226 |
-10.00 |
0.0790 |
0.4226 |
0.9029 |
-10.0000 |
0.4226 |
0.9029 |
0.0790 |
-10.0000 |
z |
2.1883 |
表E1.2 Cood. Of baseic wedge(continue)
|
74 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
75 |
Line |
Ltestl |
fct |
Lfinal |
pt1 |
xcordf |
ycordf |
zcordf |
plane |
und1-4 |
|
76 |
L1 |
0.0470 |
11.8007 |
250.97 |
1 |
0.0000 |
0.0000 |
0.0000 |
1 |
0.00 |
|
77 |
L2 |
0.1602 |
11.8007 |
147.37 |
2 |
-198.6717 |
81.3500 |
129.9981 |
2 |
0.00 |
|
78 |
L3 |
0.1968 |
11.8007 |
179.92 |
3 |
-144.0850 |
-7.5512 |
29.9981 |
3 |
0.00 |
|
79 |
L4 |
11.8007 |
11.8007 |
144.51 |
4 |
-151.0406 |
94.2856 |
25.8237 |
4 |
-118.01 |
|
80 |
L5 |
0.5119 |
11.8007 |
115.28 |
|
|
|
|
5 |
-86.47 |
|
81 |
L6 |
|
|
102.1594 |
|
|
|
|
|
|
(4)Areas of wedge, volumes of wedge and water forces:
Area of wedge surface can be computed by vector cross product, and volume of wedges and water pressure force can get from scalar triple product. Table E1.3.a is the
Spread sheet to compute water force of PT5,6,7. Table E1.3.b is the spread sheet of formulas corresponding Table E1.3.a.
Table E1.3.a Water force at PT5,6,7
|
161 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
162 |
pt |
5 |
6 |
11 |
tp1 |
tp2 |
tp3 |
v1-1 |
v2-1 |
|
163 |
x |
-110.37 |
-104.98 |
-144.09 |
-100.50 |
-104.98 |
-144.09 |
-9.87 |
-4.47 |
|
164 |
y |
45.19 |
-5.50 |
-7.55 |
8.37 |
-5.50 |
-7.55 |
36.82 |
-13.88 |
|
165 |
z |
72.22 |
21.86 |
30.00 |
113.34 |
21.86 |
30.00 |
-38.12 |
-88.48 |
|
161 |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
|
162 |
v3-1 |
v1-2 |
v2-2 |
v3-2 |
v1-3 |
v2-3 |
v3-3 |
vol |
25331.34 |
|
163 |
-43.58 |
0.00 |
-39.11 |
4.47 |
0.00 |
43.58 |
39.11 |
25331.34 |
|
|
164 |
-15.93 |
0.00 |
-2.05 |
13.88 |
0.00 |
15.93 |
2.05 |
0 |
|
|
165 |
-80.34 |
0.00 |
8.14 |
88.48 |
0.00 |
80.34 |
-8.14 |
0 |
|
Table E1.3.b Formulas of Table E 1.3.a
|
161 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
162 |
pt |
5 |
6 |
11 |
tp1 |
tp2 |
tp3 |
v1-1 |
v2-1 |
|
163 |
x |
=xpt5 |
=xpt6 |
=xpt11 |
=B163 +unx1 *hwpt5 |
=C163 +unx1 *hwpt6 |
=D163 +unx1 *hwpt11 |
=B163 -$E163 |
=C163 -$E163 |
|
164 |
y |
=ypt5 |
=ypt6 |
=ypt11 |
=B164 +uny1 *hwpt5 |
=C164 +uny1 *hwpt6 |
=D164 +uny1 *hwpt11 |
=B164 -$E164 |
=C164 -$E164 |
|
165 |
z |
=zpt5 |
=zpt6 |
=zpt11 |
=B165 +unz1 *hwpt5 |
=C165 +unz1 *hwpt6 |
=D165 +unz1 *hwpt11 |
=B165 -$E165 |
=C165 -$E165 |
|
161 |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
|
162 |
v3-1 |
v1-2 |
v2-2 |
v3-2 |
v1-3 |
v2-3 |
v3-3 |
vol |
=(Q163 +Q164 +Q165) |
|
163 |
=D163 -$E163 |
=$C163 -$F163 |
=$D163 -$F163 |
=$E163 -$F163 |
=$D163 -$G163 |
=$E163- $G163 |
=$F163 -$G163 |
=ABS (MDETERM (H163:J165) /6) |
|
|
164 |
=D164 -$E164 |
=$C164 -$F164 |
=$D164 -$F164 |
=$E164 -$F164 |
=$D164 -$G164 |
=$E164 -$G164 |
=$F164 -$G164 |
=ABS (MDETERM (K163:M165) /6) |
|
|
165 |
=D165- $E165 |
=$C165 -$F165 |
=$D165 -$F165 |
=$E165 -$F165 |
=$D165 -$G165 |
=$E165- $G165 |
=$F165 -$G165 |
=ABS (MDETERM (N163:P165) /6) |
|
|
161 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
162 |
pt |
5 |
6 |
11 |
tp1 |
tp2 |
tp3 |
v1-1 |
v2-1 |
|
163 |
x |
=xpt5 |
=xpt6 |
=xpt11 |
=B163 +unx1 *hwpt5 |
=C163 +unx1 *hwpt6 |
=D163 +unx1 *hwpt11 |
=B163 -$E163 |
=C163 -$E163 |
|
164 |
y |
=ypt5 |
=ypt6 |
=ypt11 |
=B164 +uny1 *hwpt5 |
=C164 +uny1 *hwpt6 |
=D164 +uny1 *hwpt11 |
=B164 -$E164 |
=C164 -$E164 |
|
165 |
z |
=zpt5 |
=zpt6 |
=zpt11 |
=B165 +unz1 *hwpt5 |
=C165 +unz1 *hwpt6 |
=D165 +unz1 *hwpt11 |
=B165 -$E165 |
=C165 -$E165 |
(5)Plunge of minimum safety factor during EQ:
The plunge of minimum safety factor’s computation, we use Newton iteration
method of non-linear system equation. Table E1.5a is the iteration of Newton
method, Table E1.5b is the formulas of Table E1.5.a. Generally, number of iteration should not great then 5.
Table E1.4a Driving and resisting force which excludes EQ force
|
|
B |
C |
D |
E |
F |
G |
H |
|
303 |
N1 |
N2 |
ind1 |
ind2 |
ind3 |
mxe1 |
mye1 |
|
304 |
22557.1 |
13848.7 |
1 |
0 |
0 |
0.4491 |
0.1809 |
|
303 |
I |
J |
K |
L |
M |
N |
O |
|
304 |
mze1 |
xsle1 |
ysle1 |
zsle1 |
ste1 |
Fd-noeq |
Fr-noeq |
|
|
0.5732 |
-0.7916 |
0.3241 |
0.5180 |
9213.6 |
14644.3 |
25416.3 |
Table E1.4b Formulas of Table E1.4a
|
|
I |
J |
K |
L |
M |
N |
O |
|
303 |
mze1 |
xsle1 |
ysle1 |
zsle1 |
ste1 |
Fd-noeq |
Fr-noeq |
|
304 |
=D304*Mz1 +E304*MZ2 +F304*MZ3 |
=D304*xsl1 +E304*XSL2 +F304*XSL3 |
=D304*ysl1 +E304*YSL2 +F304*YSL3 |
=D304*zsl1 +E304*ZSL2 +F304*ZSL3 |
=D304 *ST1+ E304*ST2 +F304*ST3 |
=D258*xsle1 +ysle1*E258 +zsle1*F258 |
=M304+mxe1 *D258+mye1 *E258+mze1 *F258 |
Table E1.5.a Iteration of Newton method
|
|
A |
B |
C |
D |
E |
|
306 |
K |
AA(1) |
AA(1)+360 |
AA(USE) |
BB(USE) |
|
307 |
1 |
2.7529 |
9.0361 |
2.7529 |
0.5445 |
|
308 |
|
EX |
EY |
EZ |
D1AEX |
|
309 |
|
-6333.6 |
2593.4 |
4144.3 |
-2593.4 |
|
310 |
|
D2AAEX |
D2AAEY |
D2AAEZ |
D2BBEX |
|
311 |
|
6333.6 |
-2593.4 |
0.0 |
6333.6 |
|
312 |
|
D2ABEM |
D2ABEI |
D2BBEM |
D2BBEI |
|
313 |
|
1399.0 |
0.0 |
0.0 |
-8001.0 |
|
314 |
|
F2B |
F2 |
F4A |
F4B |
|
315 |
|
0.0 |
0.1 |
0.0 |
0.4 |
Table E1.5.a Iteration of Newton method (continue)
|
|
F |
G |
H |
I |
J |
|
306 |
AA(deg) |
BB(deg) |
|
trend(eq) |
plung(eq) |
|
307 |
157.7324 |
31.1965 |
|
173.04 |
358.37 |
|
308 |
D1AEY |
D1AEZ |
D1BEX |
D1BEY |
D1BEZ |
|
309 |
-6333.6 |
0.0000 |
3835.3 |
-1570.4 |
6844.0 |
|
310 |
D2BBEY |
D2BBEZ |
D1AEM |
D1BEM |
D1AEI |
|
311 |
-2593.4 |
-4144.3 |
-2313.4 |
5361.5 |
0.0 |
|
312 |
TA |
TB |
FGA |
FGB |
F1A |
|
313 |
25416.3 |
22645.3 |
-0.1 |
0.2 |
0.1 |
|
314 |
F4 |
TP1 |
YS1 |
YS2 |
AANS(I) |
|
315 |
0.4 |
0.2 |
0.36 |
-0.65 |
3.11 |
|
|
|
|
|
|
|
Table E1.5.a Iteration of Newton method (continue)
|
|
K |
L |
M |
N |
O |
|
306 |
|
|
|
|
|
|
307 |
-1.6271 |
|
|
|
|
|
308 |
D2ABEX |
D2ABEY |
D2ABEZ |
aang(ans) |
aang(ans) |
|
309 |
1570.4 |
3835.3 |
0.0000 |
9999.00 |
999.00 |
|
310 |
D1BEI |
D2AAEM |
D2AAEI |
|
|
|
311 |
0.0000 |
2375.5 |
-5854.4 |
|
|
|
312 |
F1B |
F1 |
F2A |
|
|
|
313 |
0.3 |
0.4 |
0.062 |
|
|
|
314 |
BANS(I) |
Anga(deg) |
Angb(deg) |
ang1(del) |
ang2(del) |
|
315 |
6.17 |
178.38 |
353.77 |
20.65 |
13.55 |
Table E1.5.b Formulas of Table E1.5.a
|
|
A |
B |
C |
D |
E |
|
306 |
K |
AA(1) |
AA(1)+360 |
AA(USE) |
BB(USE) |
|
307 |
1 |
=ATAN2 (xsle1,ysle1) |
=B307+ ATAN(1)*8 |
=IF(B307<=0, C307,B307) |
=ASIN(zsle1) |
|
308 |
|
EX |
EY |
EZ |
D1AEX |
|
309 |
|
=EQF*COS(D307) *COS(E307) |
=EQF*SIN(D307) *COS(E307) |
=EQF*SIN(E307) |
=-EQF*SIN(D307) *COS(E307) |
|
310 |
|
D2AAEX |
D2AAEY |
D2AAEZ |
D2BBEX |
|
311 |
|
=-EQF*COS(D307) *COS(E307) |
=-EQF*SIN(D307) *COS(E307) |
0 |
=-EQF*COS(D307) *COS(E307) |
|
312 |
|
D2ABEM |
D2ABEI |
D2BBEM |
D2BBEI |
|
313 |
|
=K309*mxe1 +L309*mye1 +M309*mze1 |
=K309*xsle1 +L309*ysle1 +M309*zsle1 |
=E311*mxe1 +F311*mye1 +G311*mze1 |
=E311*xsle1 +F311*ysle1 +G311*zsle1 |
|
314 |
|
F2B |
F2 |
F4A |
F4B |
|
315 |
|
=-I311/G313/G313*J311 +2*F313/G313/G313/G313 *J311*K311-F313/G313 /G313*C313 |
=M313+B315 |
=D313/G313-I311 /G313/G313*K311 |
=-I311/G313/G313 *K311+2*F313/G313/ G313/G313*K311*K311 -F313/G313/G313*E313 |
Table E1.5.b Formulas of Table E1.5.a (continue)
|
|
F |
G |
H |
I |
J |
|
306 |
AA(deg) |
BB(deg) |
|
trend(eq) |
plung(eq) |
|
307 |
=D307*dac |
=E307*dac |
|
=MIN(N309,N320 N331,N342,N353) |
=MIN(O309,O320, O331,O342,O353) |
|
308 |
D1AEY |
D1AEZ |
D1BEX |
D1BEY |
D1BEZ |
|
309 |
=EQF*COS(D307) *COS(E307) |
0 |
=-EQF*COS(D307) *SIN(E307) |
=-EQF*SIN(D307) *SIN(E307) |
=EQF*COS(E307) |
|
310 |
D2BBEY |
D2BBEZ |
D1AEM |
D1BEM |
D1AEI |
|
311 |
=-EQF*SIN(D307) *COS(E307) |
=-EQF*SIN(E307) |
=E309*mxe1 +F309*mye1 +G309*mze1 |
=H309*mxe1 +I309*mye1 +J309*mze1 |
=E309*xsle1 +F309*ysle1 +G309*zsle1 |
|
312 |
TA |
TB |
FGA |
FGB |
F1A |
|
313 |
=Frnoeq1+B309 *mxe1+C309*mye1 +D309*mze1 |
=Fdnoeq1 +B309*xsle1 +C309*ysle1 +D309*zsle1 |
=H311/G313 -F313/G313 /G313*J311 |
=I311/G313 -F313/G313 /G313*K311 |
=L311/G313 -H311/G313 /G313*J311 |
|
314 |
F4 |
TP1 |
YS1 |
YS2 |
AANS(I) |
|
315 |
=D315+E315 |
=L313*F315-C315*C315 |
=-(H313*F315 -I313*C315)/G315 |
=-(L313*I313 -C315*H313)/G315 |
=MOD(D307 +H315,3.14159*2) |
(1)
Table E1.5. b Formulas of Table E1.5.a (continue)
|
|
K |
L |
M |
N |
O |
|
|
=J307-360 |
|
|
|
|
|
308 |
D2ABEX |
D2ABEY |
D2ABEZ |
aang(ans) |
aang(ans) |
|
309 |
=EQF*SIN(D307) *SIN(E307) |
=-EQF*COS(D307) *SIN(E307) |
0 |
=IF(N315<=0.05 ,L315,9999) |
=IF(N315<=0.05 ,M315,999) |
|
310 |
D1BEI |
D2AAEM |
D2AAEI |
|
|
|
311 |
=H309*xsle1 +I309*ysle1 +J309*zsle1 |
=B311*mxe1 +C311*mye1 +D311*mze1 |
=B311*xsle1 +C311*ysle1 +D311*zsle1 |
|
|
|
312 |
F1B |
F1 |
F2A |
|
|
|
313 |
=-H311/G313/G313 *J311+2*F313/G313 /G313/G313*J311*J311 -F313/G313/G313*M311 |
=J313+K313 |
=B313/G313 -H311 /G313/G313 *K311 |
|
|
|
314 |
BANS(I) |
Anga(deg) |
Angb(deg) |
ang1(del) |
ang2(del) |
|
315 |
=MOD(E307 +I315,3.14159*2) |
=J315*dac |
=K315*dac |
=ABS(F307-L315) |
=ABS(N315-G307) |
(6)Resultant force of rock wedge:
(2)
(3) Combine the wedge gravity force, water forces(PL1,PL2,PL5,……),EQ force according to different condition. Table Table E1.6 show the resultant force of rock wedge .
(4) Table E1.6 Result forces
|
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
K |
|
248 |
|
Force |
xd |
yd |
zd |
Fx |
Fy |
Fz |
|
|
|
|
249 |
weight |
28272.2 |
0.0000 |
0.0000 |
1.0000 |
0.0 |
0.0 |
28272.2 |
|
|
|
|
250 |
wtaer f1 |
6249.8 |
-0.1830 |
0.6830 |
-0.7071 |
-1143.8 |
4268.7 |
-4419.3 |
|
|
|
|
251 |
wtaer f2 |
7219.1 |
-0.5390 |
-0.7698 |
-0.3420 |
-3891.0 |
-5556.9 |
-2469.1 |
|
|
|
|
252 |
wtaer f5 |
2073.8 |
-0.9077 |
0.2432 |
-0.3420 |
-1882.3 |
504.4 |
-709.3 |
did |
dip |
|
|
253 |
E.q(1) |
8001.0 |
-0.9922 |
0.1212 |
-0.0284 |
-7938.8 |
969.7 |
-227.2 |
173.04 |
-1.6271 |
intersection of PL1&2 |
|
254 |
E.q(2) |
8001.0 |
-0.7916 |
0.3241 |
0.5180 |
-6333.6 |
2593.4 |
4144.3 |
157.73 |
31.1965 |
|
|
255 |
E.q(3) |
8001.0 |
-0.9669 |
0.0229 |
-0.2540 |
-7736.4 |
183.1 |
-2032.6 |
178.64 |
-14.7165 |
intersection of PL1&2 |
|
256 |
E.q(4) |
8001.0 |
-0.7916 |
0.3241 |
0.5180 |
-6333.6 |
2593.4 |
4144.3 |
157.73 |
31.1965 |
|
(7)Resolution of external force:
Table 1.7.a is th vector P,Q & vector M,
Table 1.7.a Vector P,Q & vector M
|
242 |
A |
B |
C |
D |
E |
F |
G |
|
243 |
case |
|
|
tpt1 |
Px |
Py |
Pz |
|
244 |
1 |
N1>=0 |
N2>=0 |
0.5090 |
0.2929 |
-0.5596 |
0.7979 |
|
245 |
2 |
N1>=0 |
N2<0 |
|
0.1830 |
-0.6830 |
0.7071 |
|
246 |
3 |
N1<0 |
N2>0 |
|
0.0000 |
0.0000 |
0.0000 |
Table 1.7.aVector P,Q & vector M(continue)
|
242 |
H |
I |
J |
K |
L |
M |
|
243 |
Qx |
Qy |
Qz |
Mx |
My |
Mz |
|
244 |
0.5933 |
0.6661 |
0.4898 |
0.4491 |
0.1809 |
0.5732 |
|
245 |
0.0000 |
0.0000 |
0.0000 |
0.0666 |
-0.2486 |
0.2574 |
|
246 |
0.5390 |
0.7698 |
0.3420 |
0.3112 |
0.4444 |
0.1975 |
(5)
Table 1.7.a Vector P,Q & vector M(continue)
|
242 |
N |
O |
P |
Q |
R |
|
243 |
ST |
xsl |
ysl |
zsl |
I_ind |
|
244 |
9213.6 |
-0.7916 |
0.3241 |
0.5180 |
1 |
|
245 |
2782.5 |
-0.1830 |
0.6830 |
0.7071 |
2 |
|
246 |
6428.1 |
-0.1962 |
-0.2802 |
0.9397 |
3 |
Table 1.7.b Formulas of Table 1.7.a
|
242 |
A |
B |
C |
D |
E |
F |
G |
|
243 |
case |
|
|
tpt1 |
Px |
Py |
Pz |
|
244 |
1 |
N1>=0 |
N2>=0 |
=unx1*uny2 -unx2*uny1 |
=((1-uix1*uix1)*uny2 +uix1*uiy1*unx2 )/D244 |
=(-(1-uiy1*uiy1)*unx2- uix1*uiy1*uny2) /D244 |
=-(uix1*uiz1*uny2 -uiz1*uiy1*unx2) /D244 |
|
245 |
2 |
N1>=0 |
N2<0 |
|
=unx1 |
=uny1 |
=unz1 |
|
246 |
3 |
N1<0 |
N2>0 |
|
0 |
0 |
0 |
(6)
Table 1.7.b Formulas of Table 1.7.a (continue)
|
242 |
H |
I |
J |
K |
L |
M |
|
243 |
Qx |
Qy |
Qz |
Mx |
My |
Mz |
|
244 |
=-((1-uix1*uix1) *uny1+uix1*uiy1 *unx1)/D244 |
=((1-uiy1*uiy1) *unx1+uix1*uiy1 *uny1)/D244 |
=(uix1*uiz1 *uny1-uiz1*uiy1 *unx1)/D244 |
=E244 *TAN(phi1*rac) +H244 *TAN(phi2*rac) |
=F244 *TAN(phi1*rac) +I244 *TAN(phi2*rac) |
=G244 *TAN(phi1*rac) +J244 *TAN(phi2*rac) |
|
245 |
0 |
0 |
0 |
=E245 *TAN(phi1*rac) +H245 *TAN(phi2*rac) |
=F245 *TAN(phi1*rac) +I245 *TAN(phi2*rac) |
=G245 *TAN(phi1*rac) +J245 *TAN(phi2*rac) |
|
246 |
=unx2 |
=uny2 |
=unz2 |
=E246 *TAN(phi1*rac) +H246 *TAN(phi2*rac) |
=F246 *TAN(phi1*rac) +I246 *TAN(phi2*rac) |
=G246 *TAN(phi1*rac) +J246 *TAN(phi2*rac) |
(7)
Table 1.7.b Formulas of Table 1.7.a (continue)
|
242 |
N |
O |
P |
Q |
R |
|
243 |
ST |
xsl |
ysl |
zsl |
I_ind |
|
244 |
=csh1*$B$242+csh2*$C$242 |
=uix1 |
=uiy1 |
=uiz1 |
1 |
|
245 |
=csh1*$B$242 |
=ux1 |
=uy1 |
=uz1 |
2 |
|
246 |
=csh2*$C$242 |
=ux2 |
=uy2 |
=uz2 |
3 |
(8)
(9) TableE1.8.a Normal forces on Pl1 & pl2
|
|
B |
C |
D |
E |
F |
G |
H |
|
257 |
csae |
load comb. |
Fxsum |
Fysum |
Fzsum |
N1I |
N2I |
|
258 |
1 |
no( Gw&Eq) |
0.00 |
0.00 |
28272.20 |
22557.12 |
13848.68 |
|
259 |
2 |
Gw(no Eq) |
-6917.11 |
-783.88 |
20674.55 |
14907.80 |
5501.38 |
|
260 |
3 |
Eq(no GW) |
-7938.80 |
969.74 |
28045.01 |
19507.74 |
9673.60 |
|
261 |
3p |
Eq(no GW) |
-6333.65 |
2593.43 |
32416.53 |
22557.12 |
13848.68 |
|
262 |
4 |
Gw&Eq |
-14653.50 |
-600.82 |
18642.00 |
10917.53 |
38.06 |
|
263 |
4p |
Gw&Eq |
-13250.8 |
1809.6 |
24818.9 |
14907.80 |
5501.38 |
(10)
(11) Table E1.8.b Formulas of TableE1.8a
|
|
B |
C |
D |
E |
F |
G |
H |
|
257 |
csae |
load comb. |
Fxsum |
Fysum |
Fzsum |
N1I |
N2I |
|
258 |
1 |
no( Gw&Eq) |
=G249 |
=H249 |
=I249 |
=D258*$E$244 +E258*$F$244 +F258*$G$244 |
=D258*$H$244 +E258*$I$244 +F258*$J$244 |
|
259 |
2 |
Gw(no Eq) |
=SUM(G249:G252) |
=SUM(H249:H252) |
=SUM(I249:I252) |
=D259*$E$244 +E259*$F$244 +F259*$G$244 |
=D259*$H$244 +E259*$I$244 +F259*$J$244 |
|
260 |
3 |
Eq(no GW) |
=G249+G253 |
=H249+H253 |
=I249+I253 |
=D260*$E$244 +E260*$F$244 +F260*$G$244 |
=D260*$H$244 +E260*$I$244 +F260*$J$244 |
|
261 |
3p |
Eq(no GW) |
=G249+G254 |
=H249+H254 |
=I249+I254 |
=D261*$E$244 +E261*$F$244 +F261*$G$244 |
=D261*$H$244 +E261*$I$244 +F261*$J$244 |
|
262 |
4 |
Gw&Eq |
=SUM(G249 :G252,G255) |
=SUM(H249 :H252,H255) |
=SUM(I249 :I252,I255) |
=D262*$E$244 +E262*$F$244 +F262*$G$244 |
=D262*$H$244 +E262*$I$244 +F262*$J$244 |
|
263 |
4p |
Gw&Eq |
=SUM(G249 :G252,G256) |
=SUM(H249 :H252,H256) |
=SUM(I249 :I252,I256) |
=D263*$E$244 +E263*$F$244 +F263*$G$244 |
=D263*$H$244 +E263*$I$244 +F263*$J$244 |
(12) (8) Safety factors:
(13)
(14) To compute the safety factors, we need judge the sliding condition, Is it sliding along intersected line of Pl1 & P2 (case 1), or sliding on dip of PL1(case 2) or Pl2(cas2 3). IF N1I>0. and N2I>0., then Isl=1, if N1I>0. and N2I<=0. then Isl=2, if N1I<=0. and N2I>0. then Isl=3,If N1I<=0. and N2I,=00. then the wedge float.
(15)
(16)
(17) Table E1.9.a Safety factors
|
272 |
A |
B |
C |
D |
E |
F |
|
273 |
case |
load comb. |
Isl |
Fd |
Fr |
Fs |
|
274 |
1 |
no( Gw&Eq) |
1 |
14644.29 |
25416.29 |
1.7356 |
|
275 |
2 |
Gw(no Eq) |
1 |
15930.42 |
17813.85 |
1.1182 |
|
276 |
3 |
Eq(no GW) |
1 |
21125.33 |
21895.92 |
1.0365 |
|
277 |
3p |
Eq(no GW) |
1 |
22645.32 |
25416.29 |
1.1224 |
|
278 |
4 |
Gw&Eq |
1 |
21061.11 |
13206.26 |
0.6270 |
|
279 |
4p |
Gw&Eq |
1 |
23931.46 |
17813.85 |
0.7443 |
(18)
(19) Table E1.9.bFormula of TableE1.9.a
|
272 |
A |
B |
C |
D |
E |
F |
|
273 |
case |
load comb. |
Isl |
Fd |
Fr |
Fs |
|
274 |
1 |
no( Gw&Eq) |
=N258 |
=D258*Q265 +E258*R265 +F258*S265 |
=P265+D258*M265 +E258*N265 +F258*O265 |
=E274/D274 |
|
275 |
2 |
Gw(no Eq) |
=N259 |
=D259*Q266 +E259*R266 +F259*S266 |
=P266+D259*M266 +E259*N266 +F259*O266 |
=E275/D275 |
|
276 |
3 |
Eq(no GW) |
=N260 |
=D260*Q267 +E260*R267 +F260*S267 |
=P267+D260*M267 +E260*N267 +F260*O267 |
=E276/D276 |
|
277 |
3p |
Eq(no GW) |
=N261 |
=D261*Q268 +E261*R268 +F261*S268 |
=P268+D261*M268 +E261*N268 +F261*O268 |
=E277/D277 |
|
278 |
4 |
Gw&Eq |
=N262 |
=D262*Q269 +E262*R269 +F262*S269 |
=P269+D262*M269 +E262*N269 +F262*O269 |
=E278/D278 |
|
279 |
4p |
Gw&Eq |
=N263 |
=D263*Q270 +E263*R270 +F263*S270 |
=P270+D263*M270 +E263*N270 +F263*O270 |
=E279/D279 |
(20)
(21) (9) Rock bolt:
(22)
(23) When safety factors are lest than the minimum required safety factors,we can use rock bot to increase the safety factors. Table E1.10.a show the required rock bolt
(24) forces and plunges for case 1,2,3,4.
(25)
(26)
(27) Table E1.10.a Rock bolt forces
|
|
F |
G |
H |
I |
J |
K |
L |
|
272 |
N1>=0, |
N2>=0 |
(case1) |
|
|
|
|
|
273 |
Fs |
trend(bolt) |
trend(bolt) |
plunge(bolt) |
bdotM |
idotm |
Boltreq |
|
274 |
1.7356 |
-13.57 |
349.43 |
-6.98 |
0.3357 |
-0.8943 |
0.0 |
|
275 |
1.1182 |
-13.57 |
349.43 |
-6.98 |
0.3357 |
-0.8943 |
3626.8 |
|
276 |
1.0365 |
-9.24 |
350.76 |
-3.83 |
0.3751 |
-0.8661 |
3708.9 |
|
277 |
1.1224 |
-9.24 |
350.76 |
-3.83 |
0.3751 |
-0.8661 |
2680.0 |
|
278 |
0.6270 |
-9.24 |
350.76 |
-3.83 |
0.3751 |
-0.8661 |
9442.5 |
|
279 |
0.7443 |
-9.24 |
350.76 |
-3.83 |
0.3751 |
-0.8661 |
8859.5 |
(28)
(29) Table E1.10.a Rock bolt forces (continue)
|
|
M |
N |
O |
P |
Q |
R |
|
272 |
N1>=0, |
N2<0 |
(case2) |
|
|
|
|
273 |
trend(bolt) |
trend(bolt) |
plunge(bolt) |
bdotM |
idotm |
Boltreq |
|
274 |
-75.00 |
285.00 |
-31.4 |
0.0858 |
-0.9718 |
0.0 |
|
275 |
-75.00 |
285.00 |
-31.4 |
0.0858 |
-0.9718 |
3940.8 |
|
276 |
-75.00 |
285.00 |
-29.4 |
0.0981 |
-0.9630 |
4123.7 |
|
277 |
-75.00 |
285.00 |
-29.4 |
0.0981 |
-0.9630 |
2979.7 |
|
278 |
-75.00 |
285.00 |
-29.4 |
0.0981 |
-0.9630 |
10498.7 |
|
279 |
4p |
-75.00 |
285.00 |
-29.4 |
0.0981 |
-0.9630 |
(30) Table E1.10.a Rock bolt forces (continue)
|
|
S |
T |
U |
V |
W |
X |
|
272 |
N1<0, |
N2>=0 |
(case3) |
|
|
|
|
273 |
trend(bolt) |
trend(bolt) |
plunge(bolt) |
bdotM |
idotm |
Boltreq |
|
274 |
55.00 |
55.00 |
-48.95 |
0.2074 |
-0.9333 |
0.0 |
|
275 |
55.00 |
55.00 |
-48.95 |
0.2074 |
-0.9333 |
3784.5 |
|
276 |
55.00 |
55.00 |
-46.05 |
0.2343 |
-0.9139 |
3913.7 |
|
277 |
55.00 |
55.00 |
-46.05 |
0.2343 |
-0.9139 |
2828.0 |
|
278 |
55.00 |
55.00 |
-46.05 |
0.2343 |
-0.9139 |
9964.0 |
|
279 |
55.00 |
55.00 |
-46.05 |
0.2343 |
-0.9139 |
9348.8 |
(31) Table E1.10.a Rock bolt forces (continue)
|
|
Y |
Z |
AA |
AB |
AC |
AD |
|
272 |
N1<0, |
N2<0 |
(case4) |
|
|
|
|
273 |
trend(bolt) |
trend(bolt) |
plunge(bolt) |
bdotM |
idotm |
Boltreq |
|
274 |
-13.57 |
349.43 |
-6.98 |
0.3357 |
-0.8943 |
0.0 |
|
275 |
-13.57 |
349.43 |
-6.98 |
0.3357 |
-0.8943 |
3626.8 |
|
276 |
-9.24 |
350.76 |
-3.83 |
0.3751 |
-0.8661 |
3708.9 |
|
277 |
-9.24 |
350.76 |
-3.83 |
0.3751 |
-0.8661 |
2680.0 |
|
278 |
-9.24 |
350.76 |
-3.83 |
0.3751 |
-0.8661 |
9442.5 |
|
279 |
-9.24 |
350.76 |
-3.83 |
0.3751 |
-0.8661 |
8859.5 |
(32)
(33) Table E1.10.b Formula of Table E1.10.a
|
|
F |
G |
H |
I |
J |
K |
L |
|
273 |
Fs |
trend(bolt) |
trend(bolt) |
plunge(bolt) |
bdotM |
idotm |
Boltreq |
|
274 |
=E274 /D274 |
=IF(indbolt=0, ATAN( (My1-fsn*ysl1) /(Mx1-fsn*xsl1) )*dac ,abotgdid) |
=IF(G274<0, G274+360 ,G274) |
=IF(indbolt=0, ATAN( (Mz1-fsn*zsl1) /(COS(H274*rac)* (Mx1-fsn*xsl1) +SIN(H274*rac) *(My1-fsn*ysl1)) )*dac ,abotgdip) |
=Mx1* COS(H274*rac) *COS(I274*rac) +My1 *SIN(H274*rac) *COS(I274*rac) +Mz1*SIN(I274*rac) |
=xsl1* COS(H274*rac) *COS(I274*rac) +ysl1 *SIN(H274*rac) *COS(I274*rac) +zsl1 *SIN(I274*rac) |
=IF(F274>=fsn ,0,(fsn*D274-E274) /(J274-fsn*K274)) |
|
275 |
=E275 /D275 |
=IF(indbolt=0, ATAN( (My1-fsn*ysl1) /(Mx1-fsn*xsl1) )*dac ,abotgdid) |
=IF(G275<0, G275+360 ,G275) |
=IF(indbolt=0 ,ATAN( (Mz1-fsn*zsl1) /(COS(H275*rac) *(Mx1-fsn*xsl1) +SIN(H275*rac) *(My1-fsn*ysl1)) )*dac ,abotgdip) |
=Mx1* COS(H275*rac) *COS(I275*rac) +My1 *SIN(H275*rac) *COS(I275*rac) +Mz1 *SIN(I275*rac) |
=xsl1* COS(H275*rac) *COS(I275*rac) +ysl1 *SIN(H275*rac) *COS(I275*rac) +zsl1 *SIN(I275*rac) |
=IF(F275>=fsn ,0,(fsn*D275-E275) /(J275-fsn*K275)) |
|
276 |
=E276 /D276 |
=IF(indbolt=0, ATAN( (My1-fse*ysl1) /(Mx1-fse*xsl1) )*dac ,abotgdid) |
=IF(G276<0, G276+360 ,G276) |
=IF(indbolt=0 ,ATAN( (Mz1-fse*zsl1) /(COS(H276*rac) *(Mx1-fse*xsl1) +SIN(H276*rac) *(My1-fse*ysl1)) )*dac ,abotgdip) |
=Mx1* COS(H276*rac) *COS(I276*rac) +My1 *SIN(H276*rac) *COS(I276*rac) +Mz1 *SIN(I276*rac) |
=xsl1* COS(H276*rac) *COS(I276*rac) +ysl1 *SIN(H276*rac) *COS(I276*rac) +zsl1 *SIN(I276*rac) |
=IF(F276>=fse, 0,(fse*D276-E276) /(J276-fse*K276)) |
|
277 |
=E277 /D277 |
=IF(indbolt=0, ATAN( (My1-fse*ysl1) /(Mx1-fse*xsl1) )*dac ,abotgdid) |
=IF(G277<0, G277+360 ,G277) |
=IF(indbolt=0, ATAN( (Mz1-fse*zsl1) /(COS(H277*rac) *(Mx1-fse*xsl1) +SIN(H277*rac) *(My1-fse*ysl1)) )*dac ,abotgdip) |
=Mx1 *COS(H277*rac) *COS(I277*rac) +My1 *SIN(H277*rac) *COS(I277*rac) +Mz1 *SIN(I277*rac) |
=xsl1* COS(H277*rac) *COS(I277*rac) +ysl1 *SIN(H277*rac) *COS(I277*rac) +zsl1 *SIN(I277*rac) |
=IF(F277>= fse,0, (fse*D277-E277) /(J277-fse*K277)) |
|
278 |
=E278 /D278 |
=IF(indbolt=0 ,ATAN( (My1-fse*ysl1) /(Mx1-fse*xsl1) )*dac ,abotgdid) |
=IF(G278<0, G278+360 ,G278) |
=IF(indbolt=0, ATAN( (Mz1-fse*zsl1) /(COS(H278*rac) *(Mx1-fse*xsl1) +SIN(H278*rac) *(My1-fse*ysl1)) )*dac ,abotgdip) |
=Mx1* COS(H278*rac) *COS(I278*rac +My1 *SIN(H278*rac) *COS(I278*rac) +Mz1 *SIN(I278*rac) |
=xsl1* COS(H278*rac) *COS(I278*rac) +ysl1 *SIN(H278*rac) *COS(I278*rac) +zsl1 *SIN(I278*rac) |
=IF(F278>= fse,0, (fse*D278-E278) /(J278-fse*K278)) |
|
279 |
=E279 /D279 |
=IF(indbolt=0, ATAN( (My1-fse*ysl1) /(Mx1-fse*xsl1) )*dac ,abotgdid) |
=IF(G279<0, G279+360 ,G279) |
=IF(indbolt=0, ATAN( (Mz1-fse*zsl1) /(COS(H279*rac) *(Mx1-fse*xsl1) +SIN(H279*rac) *(My1-fse*ysl1)) )*dac ,abotgdip) |
=Mx1 *COS(H279*rac) *COS(I279*rac) +My1 *SIN(H279*rac) *COS(I279*rac) +Mz1 *SIN(I279*rac) |
=xsl1* COS(H279*rac) *COS(I279*rac +ysl1 *SIN(H279*rac) *COS(I279*rac) +zsl1 *SIN(I279*rac) |
=IF(F279>= fse,0, (fse*D279-E279) /(J279-fse*K279)) |
(34)
(35) Table E1.10.b Formula of Table表E1.10.a (continue)
|
|
M |
N |
O |
P |
Q |
R |
|
272 |
N1>=0, |
N2<0 |
(case2) |
|
|
|
|
273 |
trend(bolt) |
trend(bolt) |
plunge(bolt) |
bdotM |
idotm |
Boltreq |
|
274 |
=IF(indbolt=0,ATAN( (MY2-fsn*YSL2) /(MX2-fsn*XSL2) )*dac,abotgdid) |
=IF(M274<0, M274+360 ,M274) |
=IF(indbolt=0,ATAN( (MZ2-fsn*ZSL2) /(COS(N274*rac) *(MX2-fsn*XSL2) +SIN(N274*rac) *(MY2-fsn*YSL2) ))*dac,abotgdip) |
=MX2 *COS(N274*rac) *COS(O274*rac) +MY2 *SIN(N274*rac) *COS(O274*rac) +MZ2 *SIN(O274*rac) |
=XSL2 *COS(N274*rac) *COS(O274*rac) +YSL2 *SIN(N274*rac) *COS(O274*rac) +ZSL2 *SIN(O274*rac) |
=IF(F274 >=fsn,0, (fsn*D274-E274) /(P274-fsn*Q274)) |
|
275 |
=IF(indbolt=0,ATAN( (MY2-fsn*YSL2) /(MX2-fsn*XSL2) )*dac,abotgdid) |
=IF(M275<0, M275+360 ,M275) |
=IF(indbolt=0,ATAN( (MZ2-fsn*ZSL2)/ (COS(N275*rac) *(MX2-fsn*XSL2) +SIN(N275*rac) *(MY2-fsn*YSL2)) )*dac,abotgdip) |
=MX2 *COS(N275*rac) *COS(O275*rac) +MY2 *SIN(N275*rac) OS(O275*rac) +MZ2 *SIN(O275*rac) |
=XSL2 *COS(N275*rac)* COS(O275*rac) +YSL2 *SIN(N275*rac) *COS(O275*rac) +ZSL2 *SIN(O275*rac) |
=IF(F275>= fsn,0, (fsn*D275-E275) /(P275-fsn*Q275)) |
|
276 |
=IF(indbolt=0,ATAN( (MY2-fse*YSL2) /(MX2-fse*XSL2) )*dac,abotgdid) |
=IF(M276<0, M276+360 ,M276) |
=IF(indbolt=0,ATAN( (MZ2-fse*ZSL2) /(COS(N276*rac) *(MX2-fse*XSL2) +SIN(N276*rac )*(MY2-fse*YSL2)) )*dac,abotgdip) |
=MX2 *COS(N276*rac) *COS(O276*rac) +MY2 *SIN(N276*rac) *COS(O276*rac) +MZ2 *SIN(O276*rac) |
=XSL2 *COS(N276*rac) *COS(O276*rac) +YSL2 *SIN(N276*rac) *COS(O276*rac) +ZSL2 *SIN(O276*rac) |
=IF(F276>=fse,0, (fse*D276-E276) /(P276-fse*Q276)) |
|
277 |
=IF(indbolt=0,ATAN( (MY2-fse*YSL2) /(MX2-fse*XSL2 ))*dac,abotgdid) |
=IF(M277<0, M277+360 ,M277) |
=IF(indbolt=0,ATAN( (MZ2-fse*ZSL2) /(COS(N277*rac) *(MX2-fse*XSL2) +SIN(N277*rac) *(MY2-fse*YSL2)) )*dac,abotgdip) |
=MX2* COS(N277*rac) *COS(O277*rac) +MY2 *SIN(N277*rac) *COS(O277*rac) +MZ2 *SIN(O277*rac) |
=XSL2 *COS(N277*rac) *COS(O277*rac) +YSL2 *SIN(N277*rac) *COS(O277*rac) +ZSL2 *SIN(O277*rac) |
=IF(F277>=fse,0, (fse*D277-E277)/ (P277-fse*Q277)) |
|
278 |
=IF(indbolt=0,ATAN( (MY2-fse*YSL2) /(MX2-fse*XSL2)) *dac,abotgdid) |
=IF(M278<0, M278+360 ,M278) |
=IF(indbolt=0,ATAN( (MZ2-fse*ZSL2) /(COS(N278*rac) *(MX2-fse*XSL2) +SIN(N278*rac) *(MY2-fse*YSL2)) )*dac,abotgdip) |
=MX2* COS(N278*rac) *COS(O278*rac) +MY2 *SIN(N278*rac) *COS(O278*rac) +MZ2 *SIN(O278*rac) |
=XSL2 *COS(N278*rac) *COS(O278*rac) +YSL2 *SIN(N278*rac) *COS(O278*rac) +ZSL2 *SIN(O278*rac) |
=IF(F278>=fse,0, (fse*D278-E278) /(P278-fse*Q278)) |
|
(36) 279 |
=IF(indbolt=0,ATAN( (MY2-fse*YSL2) /(MX2-fse*XSL2) )*dac,abotgdid) |
=IF(M279<0, M279+360 ,M279) |
=IF(indbolt=0,ATAN( (MZ2-fse*ZSL2) /(COS(N279*rac) *(MX2-fse*XSL2) +SIN(N279*rac) *(MY2-fse*YSL2)) )*dac,abotgdip) |
=MX2* COS(N279*rac) *COS(O279*rac) +MY2* SIN(N279*rac) *COS(O279*rac) +MZ2* SIN(O279*rac) |
=XSL2 *COS(N279*rac) *COS(O279*rac) +YSL2 *SIN(N279*rac) *COS(O279*rac) +ZSL2 *SIN(O279*rac) |
=IF(F279>=fse,0, (fse*D279-E279) /(P279-fse*Q279)) |
(37)
(38) (10) Plane views of plane xy, y(-z), x(-z)
(39) The charts of rock wedge are plotted by Excel x-y scatter chart method.
(40)
(41) 表E1.11
|
|
y |
x |
-z |
y |
-z |
x |
|
pt1 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.0000 |
|
pt2 |
81.350 |
-198.672 |
-129.998 |
81.350 |
-129.998 |
-198.6717 |
|
pt1 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.0000 |
|
pt3 |
-7.551 |
-144.085 |
-29.998 |
-7.551 |
-29.998 |
-144.0850 |
|
pt2 |
81.350 |
-198.672 |
-129.998 |
81.350 |
-129.998 |
-198.6717 |
|
pt4 |
94.286 |
-151.041 |
-25.824 |
94.286 |
-25.824 |
-151.0406 |
|
pt1 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.0000 |
|
pt5 |
45.193 |
-110.370 |
-72.219 |
45.193 |
-72.219 |
-110.3699 |
|
pt6 |
-5.502 |
-104.976 |
-21.856 |
-5.502 |
-21.856 |
-104.9762 |
|
pt7 |
53.924 |
-86.383 |
-14.769 |
53.924 |
-14.769 |
-86.3829 |
|
pt5 |
45.193 |
-113.370 |
-72.219 |
45.193 |
-72.219 |
-113.3699 |
|
pt8 |
81.350 |
-198.672 |
-129.998 |
81.350 |
-129.998 |
-198.6717 |
|
pt9 |
81.350 |
-198.672 |
-129.998 |
81.350 |
-129.998 |
-198.6717 |
|
pt10 |
81.350 |
-198.672 |
-129.998 |
81.350 |
-129.998 |
-198.6717 |
|
pt8 |
81.350 |
-198.672 |
-129.998 |
81.350 |
-129.998 |
-198.6717 |
|
pt2 |
81.350 |
-198.672 |
-129.998 |
81.350 |
-129.998 |
-198.6717 |
|
pt12 |
-7.551 |
-144.085 |
-29.998 |
-7.551 |
-29.998 |
-144.0850 |
|
pt11 |
-7.551 |
-144.085 |
-29.998 |
-7.551 |
-29.998 |
-144.0850 |
|
pt13 |
-7.551 |
-144.085 |
-29.998 |
-7.551 |
-29.998 |
-144.0850 |
|
pt12 |
-7.551 |
-144.085 |
-29.998 |
-7.551 |
-29.998 |
-144.0850 |
|
pt13 |
-7.551 |
-144.085 |
-29.998 |
-7.551 |
-29.998 |
-144.0850 |
|
pt3 |
-7.551 |
-144.085 |
-29.998 |
-7.551 |
-29.998 |
-144.0850 |
|
pt16 |
94.286 |
-151.041 |
-25.824 |
94.286 |
-25.824 |
-151.0406 |
|
pt14 |
94.286 |
-151.041 |
-25.824 |
94.286 |
-25.824 |
-151.0406 |
|
pt15 |
94.286 |
-151.041 |
-25.824 |
94.286 |
-25.824 |
-151.0406 |
|
pt16 |
94.286 |
-151.041 |
-25.824 |
94.286 |
-25.824 |
-151.0406 |
|
pt4 |
94.286 |
-151.041 |
-25.824 |
94.286 |
-25.824 |
-151.0406 |
(42)
(43)

(44) Figure E1.2.a xy Plane view
(45)

(46) Figure E1.2.b y(-z) plane view
(47)

(48) FigureE1.2.c x(-z) plane view
(49)
(50) (11) Spread sheets:
(51)
(52) Hereafter are all the spread sheets to be used in the stability analysis of rock wedge failure developed by the Arthur.
(53)



(54)










(55)

(56)


(57)




(58) Figure E1.3
上次修改此網站的日期: 2018年12月02日