2019年03月23日

VB program of rotation and reflection in 3D space

Rotation in 3D space

     To rotate a point around a arbitrarily line is quite simple and easy just using the sub m3RotAboutLineGetPtxyzA()(after Glenn Murray, Colorado School of Mines) or function m3RotAboutLineGetPtxyz(), and to rotate a profile or a surface , you can apply the transformation operation to all the points of curve or surface.

Figure 1

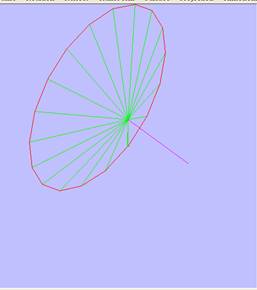
Figure 2

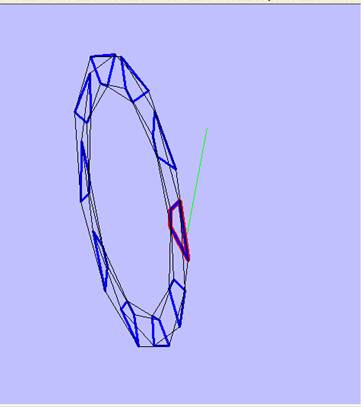
Figure 3

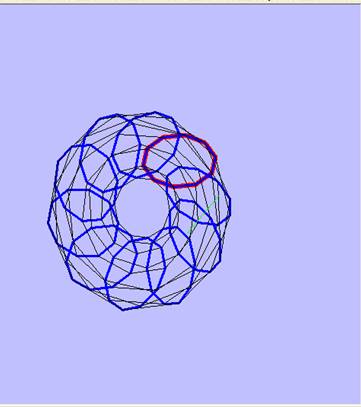
Figure 4

In Figure 3 and figure 4, the red solid lines are profile of base profile curve, the green

lines are line of rotation axis.

The following snippet codes of Function m3RotAboutLineGetPtxyz

Public Function m3RotAboutLineGetPtxyz(ByRef ptRotBeg As ptXyz, ByRef ptRotEnd As ptXyz, ByRef PtIn As ptXyz, ByVal CitaDeg As Single) ptXyz

‘Glenn Murray,Coloado School of Mines

Dim a As Single, b As Single, c As Single, U As Single, V As Single, W As Single, CitaR As Single, L As Single

Dim Xin As Single, Yin As Single, Zin As Single

Dim ptOut as ptXyz

a = ptRotBeg.x

        b = ptRotBeg.y

        c = ptRotBeg.z

        U = ptRotEnd.x - ptRotBeg.x

        V = ptRotEnd.y - ptRotBeg.y

        W = ptRotEnd.z - ptRotBeg.z

        Xin = PtIn.x

        Yin = PtIn.y

        Zin = PtIn.z

        CitaR = CitaDeg * PI / 180#

        L = Sqr(U ^ 2 + V ^ 2 + W ^ 2)

        ptOut.x = (a * (L ^ 2 - U ^ 2) + U * (-b * V - c * W + U * Xin + V * Yin + W * Zin) + ((Xin - a) * (L ^ 2 - U ^ 2) + U * (b * V + c * W - V * Yin - W * Zin)) * Cos(CitaR)+ L * (-c * V + b * W - W * Yin + V * Zin) * Sin(CitaR)) / L ^ 2

        ptOut.y = (b * (L ^ 2 - V ^ 2) + V * (-a * U - c * W + U * Xin + V * Yin + W * Zin) + ((Yin - b) * (L ^ 2 - V ^ 2) + V * (a * U + c * W - U * Xin - W * Zin)) * Cos(CitaR) + L * (c * U - a * W + W * Xin - U * Zin) * Sin(CitaR)) / L ^ 2

        ptOut.z = (c * (L ^ 2 - W ^ 2) + W * (-a * U - b * V + U * Xin + V * Yin + W * Zin) + ((Zin - c) * (L ^ 2 - W ^ 2) + W * (a * U + b * V - U * Xin - V * Yin)) * Cos(CitaR) + L * (-b * U + a * V - V * Xin + U * Yin) * Sin(CitaR)) / L ^ 2

      Function m3RotAboutLineGetPtxyz=ptOut

    End Function

Reflection in 3D space

Reflection a point across a line in 2D plane (Figure 5) can apply the translations and rotations operation to get the answer point, or find the closest point(F) to the line (AB) and then extend twice distance of the line[PF, connecting the origin point(P) and closest point(F)] to get point P’, then point P’ is the reflection of point P across line AB.

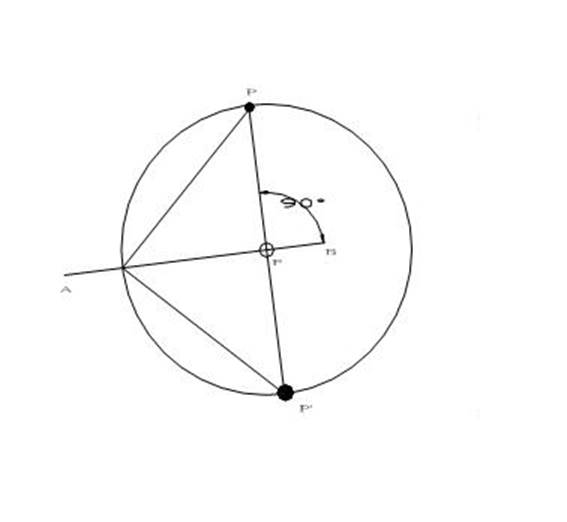
Figure 5

The following VB 6.0 snippet codes are the sub to find the reflection point across a line in 2d space.

Type CadPoint ‘same as PointF in VB.NET

X as single,

Y assingle

End Type

Type CadLine

Pts(0) as CadPoint

Pts(1) as Cadpoint

End Type

Public Function ReflectPointA(ByRef myPoint As CadPoint, ByRef mybaseline As cadLine) As CadPoint

       ReflectPointA = myPoint

       Dim ptvert As CadPoint

       Dim extLine As cadLine

       extLine = lineEndExtendBothEnd(mybaseline, 1000)

       ptvert = ClosestPtOnLineToReferPt(myPoint, extLine, True)  '

       Dim Ldist As Single

       Ldist = ptptLen(myPoint, ptvert)

       MsgBox ("ldist=" & Ldist)

       ReflectPointA = ptOnLine_GivenDist(myPoint, ptvert, 2 * Ldist)

End Function

Function lineEndExtendBothEnd(ByRef myLine As cadLine, ByVal dist As Single) As cadLine

        lineEndExtendBothEnd = myLine

        lineEndExtendBothEnd.pts(0) = ptOnLine_GivenDist(myLine.pts(1), myLine.pts(0), dist)

        lineEndExtendBothEnd.pts(1) = ptOnLine_GivenDist(myLine.pts(0), myLine.pts(1), dist)

    End Function

Function ptOnLine_GivenDist(ByRef ptFrom As CadPoint, ByRef ptToEnd As CadPoint, ByVal myDistFromStart As Single) As CadPoint

        Dim Lline As Single

        Lline = ptptLen(ptFrom, ptToEnd)

        ptOnLine_GivenDist.X = ptFrom.X + (ptToEnd.X - ptFrom.X) * myDistFromStart / Lline

        ptOnLine_GivenDist.Y = ptFrom.Y + (ptToEnd.Y - ptFrom.Y) * myDistFromStart / Lline

    End Function

Private Function ClosestPtOnLineToReferPt(ByRef referPt As CadPoint, ByRef myLine As cadLine, Optional ByRef isRealPtIn As Boolean = True) As CadPoint 

’find a closest point to a line from a given point(已知線外一點求垂線座標垂足點)

Dim aX As Single, aY As Single, Bx, By As Single, px As Single, py As Single, Ldist As Single

Dim vAB_x As Single, vAB_y As Single, uAB_x As Single, uAB_y As Single, vPA_x As Single, vPA_y As Single, ptvert As CadPoint

Dim t As Single, isPtonLine As Boolean, Ltl As Single, L1 As Single, L2 As Single ', ptVert As CadLine

     Bx = myLine.Vertex(1).X

     By = myLine.Vertex(1).Y

     aX = myLine.Vertex(0).X

     aY = myLine.Vertex(0).Y

     px = referPt.X

     py = referPt.Y

     vAB_x = Bx - aX

     vAB_y = By - aY

     Ldist = Sqr(vAB_x ^ 2 + vAB_y ^ 2)

     If Ldist <= 0.0001 Then Exit Function

     uAB_x = vAB_x / Ldist  ' x comp. of unit vector(uab)單位向量 uab的x分量

     uAB_y = vAB_y / Ldist 'y comp. of unit vector(uab) 單位向量 uab的y分量

     vPA_x = px - aX

     vPA_y = py - aY

     t = uAB_x * vPA_x + uAB_y * vPA_y

     ptvert.X = aX + t * uAB_x

     ptvert.Y = aY + t * uAB_y

     If isRealPtIn = False Then

     ClosestPtOnLineToReferPt = ptvert

     Exit Function

     End If

     'Check point on line

     If isRealPtIn = True Then

     If IsPtOnLine_ByPoint(myLine, ptvert) Then

      ClosestPtOnLineToReferPt = ptvert

      Else

       ClosestPtOnLineToReferPt.X = 99999999#

       ClosestPtOnLineToReferPt.Y = 99999999#

      End If

     End If

 In 3D space(Figure 6), the reflection of a point(P) across a arbitrarily line(AB) are more complicated by using transformation matrix operation, but we can simple rotate the point[P(x,y,z)] around line(OA) through 180° to get the desired point[P’(xf,yf,zf)].

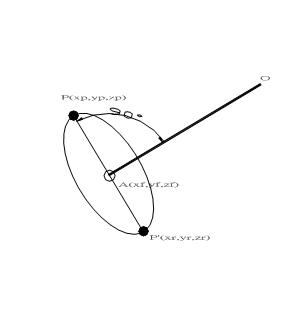
Figure 6

In figure 7, drawing a line from point [G(xg,yg,zg)] parallel to the normal N(a,b,c) of plane ABCD, this line penetrate the plane at point [P(x,y,z)], then line GB can be defined as:

x=xg+t*a :y=yg_t*b:z=zg+t*c

substituting x,y,z into palne ax+by+cz=d ,we can get

t=(d-a*xg-b*yg-c*zg)/(a^2+b^2+c^2) and

x=xg+a*(d-a*xg-b*yg-c*zg)/(a^2+b^2+c^2)

y=yg+b*(d-a*xg-b*yg-c*zg)/(a^2+b^2+c^2)

z=zg+c*(d-a*xg-b*yg-c*zg)/(a^2+b^2+c^2)

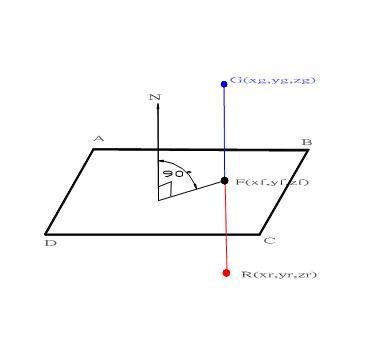
Figure 7

The following snippet codes are the sub programs to implement of reflection of a point across a line, a point across a plane.

Type ptXyz

X as single

Y as single

Z as single

End Type

(a) Reflect a point across a line

Public Function ptXyzReflection_Rot(myLineXyz As LineXyz, PtIn As ptXyz, Optional chk As Single = 0#) As ptXyz

        Dim ptRotBeg As ptXyz

        Dim ptRotEnd As ptXyz

        Dim ptReflect As ptXyz

        ptRotBeg = myLineXyz.pts(0)

        ptRotEnd = myLineXyz.pts(1)

        Call m3RotAboutLineGetPtxyzA(ptRotBeg, ptRotEnd, PtIn, 180, ptReflect)

        ptXyzReflection_Rot = ptReflect

        Dim delx1 As Single, dely1 As Single, delZ1 As Single

        Dim delx2 As Single, dely2 As Single, delZ2 As Single

        delx1 = myLineXyz.pts(1).x - myLineXyz.pts(0).x

        dely1 = myLineXyz.pts(1).y - myLineXyz.pts(0).y

        delZ1 = myLineXyz.pts(1).z - myLineXyz.pts(0).z

        delx2 = ptXyzReflection_Rot.x - PtIn.x

        dely2 = ptXyzReflection_Rot.y - PtIn.y

        delZ2 = ptXyzReflection_Rot.z - PtIn.z

        chk = Abs(delx1 * delx2 + dely1 * dely2 + delZ1 * delZ2)

        If chk >= 0.01 Then MsgBox ("Err= " & chk)

    End Function

(b) Rotate a point around a line

Public Sub m3RotAboutLineGetPtxyzA(ByRef ptRotBeg As ptXyz, ByRef ptRotEnd As ptXyz, ByRef PtIn As ptXyz, ByVal CitaDeg As Single, ByRef ptOut As ptXyz)

‘after Glenn Murray,Coloado School of Mines

Dim a As Single, b As Single, c As Single, U As Single, V As Single, W As Single, CitaR As Single, L As Single

Dim Xin As Single, Yin As Single, Zin As Single

a = ptRotBeg.x

        b = ptRotBeg.y

        c = ptRotBeg.z

        U = ptRotEnd.x - ptRotBeg.x

        V = ptRotEnd.y - ptRotBeg.y

        W = ptRotEnd.z - ptRotBeg.z

        Xin = PtIn.x

        Yin = PtIn.y

        Zin = PtIn.z

        CitaR = CitaDeg * PI / 180#

        L = Sqr(U ^ 2 + V ^ 2 + W ^ 2)

        ptOut.x = (a * (L ^ 2 - U ^ 2) + U * (-b * V - c * W + U * Xin + V * Yin + W * Zin) + ((Xin - a) * (L ^ 2 - U ^ 2) + U * (b * V + c * W - V * Yin - W * Zin)) * Cos(CitaR) _

                + L * (-c * V + b * W - W * Yin + V * Zin) * Sin(CitaR)) / L ^ 2

        ptOut.y = (b * (L ^ 2 - V ^ 2) + V * (-a * U - c * W + U * Xin + V * Yin + W * Zin) + ((Yin - b) * (L ^ 2 - V ^ 2) + V * (a * U + c * W - U * Xin - W * Zin)) * Cos(CitaR) _

                + L * (c * U - a * W + W * Xin - U * Zin) * Sin(CitaR)) / L ^ 2

        ptOut.z = (c * (L ^ 2 - W ^ 2) + W * (-a * U - b * V + U * Xin + V * Yin + W * Zin) + ((Zin - c) * (L ^ 2 - W ^ 2) + W * (a * U + b * V - U * Xin - V * Yin)) * Cos(CitaR) _

                + L * (-b * U + a * V - V * Xin + U * Yin) * Sin(CitaR)) / L ^ 2

    End Sub

While the reflection of a point G(xg,yg,zg) about a plane ABCD, we can draw a line parallel to the plane normal and get the penetrating point(F) and extend to the point to let GF=FR.

(c) Reflect a point across a plane

Public Function PtxyzReflection_plane(a As Single, b As Single, c As Single, d As Single, ptOutside As ptXyz) As ptXyz

        'ax+by+cz=d

         Dim ptFoot As ptXyz

         Dim L As Single

         ptFoot = ClosestPtToPlane(a, b, c, d, ptOutside)

         L = ptptLenXyz(ptOutside, ptFoot)

         PtxyzReflection_plane = ptxyzOnLineXyz_GivenDist(ptOutside, ptFoot, 2 * L)

  End Function

Public Function ClosestPtToPlane(a As Single, b As Single, c As Single, d As Single, ptOutside As ptXyz) As ptXyz

        'ax+by+cz=d

         Dim t As Single

         t = (d - ptOutside.x * a - ptOutside.y * b - ptOutside.z * c) / (a ^ 2 + b ^ 2 + c ^ 2)

         ClosestPtToPlane.x = ptOutside.x + t * a

         ClosestPtToPlane.y = ptOutside.y + t * b

         ClosestPtToPlane.z = ptOutside.z + t * c

  End Function

Public Function ptxyzOnLineXyz_GivenDist(ptxyzBeg As ptXyz, ptxyzEnd As ptXyz, distFromBeg As Single) As ptXyz

        Dim Lt As Double

        Lt = ptptLenXyz(ptxyzBeg, ptxyzEnd)

        If Lt <= 0.01 Then

        MsgBox ("err in ptxyzOnLineXyz_GivenDist ;pt1= " & ptXyzToString(ptxyzBeg) & "; pt2= " & ptXyzToString(ptxyzEnd))

        End If

        ptxyzOnLineXyz_GivenDist.x = ptxyzBeg.x + (ptxyzEnd.x - ptxyzBeg.x) *

distFromBeg / Lt

        ptxyzOnLineXyz_GivenDist.y = ptxyzBeg.y + (ptxyzEnd.y - ptxyzBeg.y) * distFromBeg / Lt

        ptxyzOnLineXyz_GivenDist.z = ptxyzBeg.z + (ptxyzEnd.z - ptxyzBeg.z) * distFromBeg / Lt

    End Function

Figure 8

Figure 9

Figure 10

In figure 10, the blue surface is the drawing of function z=x^2+y^2-16, the red surface

is the reflection curve of z=x^2+y^2-16, while the black is the combination of  reflection and translation of the original surface.

For more information, please link www.chday169.url.tw

Name(您的大名)
E_MAIL(您的電子信箱)
Comment or Suggestion(您想反應的狀況，建議，或諮詢事項)