User defined Ellipse Function in Python Canvas

使用者自定橢圓函數

                               By daych169

(1)            Introduction:

After using Python canvas to draw widget shapes , I find out

(1)  pure python canvas cannot use’ floodfill ‘ method to fill a irregular region surrounding by primitive shapes.(2)canvas can only save the shapes to printer postscript file, which could not redraw again,(3)The methods such as find_closest ,  find_enclosed , find_withtag, etc. hard to edit or modify a primitive shape in canvas directly. These issues mentioned above can implement easily in vb6. So I plan to solve it follow the concepts similar to the programs I designed before. First, we need to classify the canvas primitive to four basic types (a)line(lines), (b)polygons,(c)texts, (4) images. Here we will focus on line and polygon only. Classify circle arc, open ellipse , polyline, spline and other non_closed shapes as line, and  closed shapes, such as ellipse ,circle ,rectangle ,triangle ,closed polygon ,closed spline as polygon. Because Python Canvas polygon method can use optional attitudes ‘stipple ‘ to fill irregular region with predefined stipple or pattern(xbm or XBM file), to fill colors on any closed region ,using ’activefill’to show a color when mouse move over the shape. Following are the shapes plotted by author’s   progrm(vb 6).

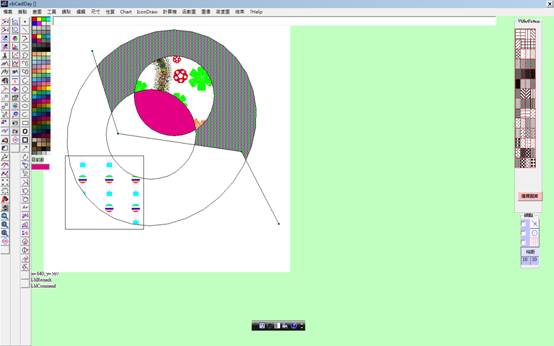學習Python tkinter canvas s畫圖後，發現(1)使用canvas在由兩

個圖元(primitive)以上所組成之不規則區域，無法直接在圖上使用洪溢填充方法(Floodfill,fill)鋪貼預設圖案、自定圖案或顏色，(2) canvas畫完圖後想再行編輯及改變性質(edit primitive & modify properties)，所能使用之工具相當有限及困難，(3)canvas只能將圖元儲存成印表機認識之postscript 文字檔，似乎無法直接儲存成canvas相容之圖檔，需要時，能轉譯再繪成為原圖(redraw)。上述問題在vb6中實現並不困難，上圖就是我用vb6所設計之cad程式所繪製之圖案。因為有vb6之設計觀念，在研習多日後，終於研究出解決方法。利用tkinter canvas所有提供之資源，實現解決方案。

Before introduce the user defined ellipse widget. I want to introduce line draw method offer by Python tkinter(Tkinter) briefly. We are going to implement the ellipse curve by canvas. create_line or canvas. create_polygon method. The widget of python canvas supplies graphics facilities for Tkinter(tkinter) .Among these graphical objects are texts, lines, circles,polygons,ovals,arc,rectangle,windows, images, and other widgets. With this widget it's possible to draw graphs and plots, create primitive graphics editors, and implement various kinds of user_defined widgets. 

id = canvas.create_line(x0, y0, x1, y1, ..., xn, yn, option, ...)

The line goes through a series of points (x0,y0), (x1, y1), … (xn, yn).The method create_line is used to draw a straight line or polyline. The coordinates "coords" are given as four integer numbers: (x0, y0, x1, y1 )for a line ,and (x0,y0,x1,y1,x2,y2,x3,y3,….. ) for a polyline or smooth curve_fitting polyline(set smooth=True) under the same name ‘line’. This means that the line goes from the point (x0, y0) to the point (x1,y1, ) ,and from (x0, y0) to (x1, y1) and then to (x2, y2)…….. for a polyline. After these coordinates follows a comma separated these list of additional optional parameters, which may be empty or ‘None’. For example ,We can draw a line with penwidth=3, color=’red’.This can be implemented something like id=canvas.create_line(50,50,200,200,width=3,fill=’red’,arrow=None,activefill=’green’). Here create_line is the method of drawing by Python Tkiner, (50,50,200,200) is the coords ,width is the keyword for pen size, fill is the keyword of pen color, arrow is the keyword of arrow of line(can be ‘tk.FIRST’,’tk.LAST’,’tk.BOTH’), and actiivefill is the color of line when cursor moving over the line, id is the return handler of line.

The options for polygon are quite similar to line, some useful options,such as ‘stipple’,’outline’,’fill’are different with line. ‘fill’is used to fill the enclosed region,’outline’ is the color of polygon boundary line,’stipple’ is the stipple or predefined pattern to tile a closed region. The following diagrams are plotted by Arthur designed python program. The irregular closed regional area are detected first, and then it can be tiled with predefined stipple pattern or user_ defined pattern. Since the coordinates are found out, so the boundary line length and area can be calculated as well. The algorithm of detective method and xbp file making method and procedures are  another interesting issues, I would like to share friends in the future.

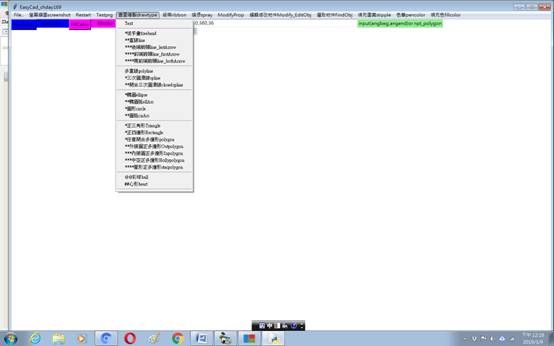
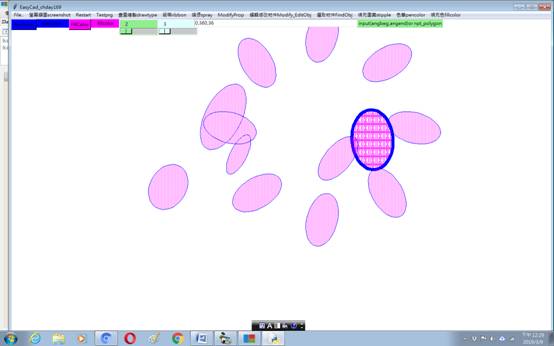
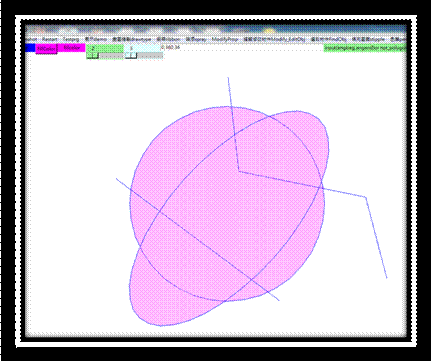
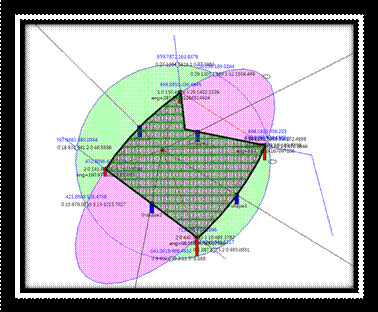
　　Python tkinter自帶畫圖方法雖然可以繪製橢圓圖形，但只能畫垂直或水平，如要畫傾斜橢圓圖形，必須借用第三方提供之函數，如numpy，matplotlib等， 如要編輯或修改圖形相當不方便。本文所要討論的是，如何使用自訂函數繪製及編輯橢圓曲線。

(2)Governing equation of Ellipse and Ellipse arc:

The arc or oval methods offered by Python canvas can only draw the arc or oval curves enclosed by a box. If you intend to draw an inclined ellipse curve , You need to import numpy , matplotlib , PIL. ,

wxpython. Hereafetr,  I like to discuss a user defined function to draw ellipse by mouse or given three points to get an ellipse, simple and easily. And you also can draw an ellipse rubber_band ellipse or ellipse arc. The governing equation of ellipse curve can be defined like:

橢圓形曲線之方程式為：

(x-xc)**2/a**2 +(y-yc)/b**2=1

or

x=xc+a*cos(theta)  y=yc+b*sin(theta)

通過平面上三個座標點可以定義一個傾斜之橢圓曲線。

Here (xc,yc) is the center of ellipse

a ,b is the semi diameter of long and short axis respectively.

If we give a three points(x0,y0),(x1,y1),(x2,y2) on a ellipse curve then

We can get :

xcen(xc)=(x0+x1)/2,

ycen(yc)=(y0+y1)/2

a= sqrt((x0 - xcen)**2 + (y0 - yeny) **2)

theta =atan2((y1-y0), (x1-x0))

b can be obtained after a, theta be solved.

def ellipse_Prop(x0,y0,x1,y1,x2,y2):

    ptcenx=(x0+x1) / 2.  # center of ellipse

    ptceny=(y0+y1) / 2.

    #print("ptcen.x,ptcen.y",ptcenx,ptceny)

    angslop = math.degrees(math.atan2((y1-y0), (x1-x0)))

    #print( 'angslop=',angslop)

    aa = math.sqrt((x0 - ptcenx)**2 + (y0 - ptceny) **2)

    #print('aa',aa)

    ptanyx = x2

    ptanyy = y2

    #print('ptany=',ptany.x,ptany.y)

    ta1 = ptanyx - ptcenx

    ta2 = aa * math.cos(math.radians(angslop))

    ta3 = -math.sin(math.radians(angslop))

    #print('ta1,ta2,ta3',ta1,ta2,ta3)

    tb1 = ptanyy - ptceny

    tb2 = aa * math.sin(math.radians(angslop))

    tb3 = math.cos(math.radians(angslop))

    #print('tb1,tb2,tb3',tb1,tb2,tb3)

    t1 = (ta1 * tb3 - tb1 * ta3) / (ta2 * tb3 - ta3 * tb2)

    t2 = (ta2 * tb1 - tb2 * ta1) / (ta2 * tb3 - ta3 * tb2)

    #print("t1,t2",t1,t2)

    #print(1-t1**2)

    bb=0

    if (1.0-t1**2) >= 0.00001 :

        bb = math.sqrt(t2**2 / (1.0 - t1 ** 2))

        #print("bb",bb)

    else:

        print("error in function ellprop")

    #print('aa,bb',aa,bb)

    #xys=[ptcenx,ptceny,aa,bb,angslop]

    #return xys #ptcenx,ptceny,aa,bb,angslop

    return ptcenx,ptceny,aa,bb,angslop

#-----------------------------------------------------------------

def ellipsemaker_XY(x0,y0,x1,y1,x2,y2,angbeg,angend,npt,cenReturn=0):

# angbeg,angend are angles of ellipse beg. & end of curve

# npt are no. of point on ellipse

# cenReturn=1, return (ptcenx,ptceny)

    #print('x0,y0,x1,y1,x2,y2',x0,y0,x1,y1,x2,y2)

    ptcenx=(x0+x1) / 2.

    ptceny=(y0+y1) / 2.

    #print("ptcen.x,ptcen.y",ptcen.x,ptcen.y)

    angslop = math.degrees(math.atan2((y1-y0), (x1-x0)))

    #print( 'angslop=',angslop)

    aa = math.sqrt((x0 - ptcenx)**2 + (y0 - ptceny) **2)

    #print('aa',aa)

    ptanyx = x2

    ptanyy = y2

    #print('ptany=',ptany.x,ptany.y)

    ta1 = ptanyx - ptcenx

    ta2 = aa * math.cos(math.radians(angslop))

    ta3 = -math.sin(math.radians(angslop))

    tb1 = ptanyy - ptceny

    tb2 = aa * math.sin(math.radians(angslop))

    tb3 = math.cos(math.radians(angslop))

    t1 = (ta1 * tb3 - tb1 * ta3) / (ta2 * tb3 - ta3 * tb2)

    t2 = (ta2 * tb1 - tb2 * ta1) / (ta2 * tb3 - ta3 * tb2)

      bb=aa

    try:

        if (1.0-t1**2) >= 0.0000001 :

            bb = math.sqrt(t2**2 / (1.0 - t1 ** 2))

        else:

            #print("error in function ellprop")

            pass

    except:

        pass

    ndo=npt

    ang0=angbeg

    ang1=angend

   if ang1 == 0.0 :

        ang1= 359.999999

    if ang1 < ang0 :

        ang1 =ang1+360.0

    angbeg=ang0

    angend=ang1

    delang = (angend-angbeg) / npt

   xout=[]

    yout=[]

    pts=[]

    for i in range(0,ndo):

        angi = angbeg + delang * i

        tpt1=aa* math.cos(math.radians(angi))* math.cos(math.radians(angslop))

        tpt2=- bb * math.sin(math.radians(angi)) * math.sin(math.radians(angslop))   # 'xcoord(x座標)

        ptsix=tpt1+tpt2

        tpt3=aa* math.cos(math.radians(angi))* math.sin(math.radians(angslop))

        tpt4= bb * math.sin(math.radians(angi)) * math.cos(math.radians(angslop))   # 'ycoord(y座標)

        ptsiy=tpt3 +tpt4

        ptsix=ptcenx+ptsix

        ptsiy=ptceny+ptsiy

        xout.append(ptsix)

        yout.append(ptsiy)

        pts += (ptsix,ptsiy)

        #print("ptellp",i,ptellp[i].x,ptellp[i].y)

    if cenReturn==0:

        if abs(360-abs(angend-angbeg))<=0.01 :

            xout.append(xout[0])

            yout.append(yout[0])

            pts +=(xout[0],yout[0])

            return npt+1,xout,yout,pts

        else:

            return npt,xout,yout,pts

    else:

        if abs(360-abs(angend-angbeg))<=0.01 :

            xout.append(xout[0])

            yout.append(yout[0])

            pts +=(xout[0],yout[0])

            return npt+1,xout,yout,pts,ptcenx,ptceny

        else:

            return npt,xout,yout,pts,ptcenx,ptceny

#----------------------------------------------------

The ellipse drawing by python canvas like:

Canvas.create_oval(xmin,ymin,xmax,ymax)

is same as

x0,y0=xmin,(ymin+ymax)/2

x1,y1=xmax,(ymin+ymax)/2

x2,y2=(xmin+xmax)/2,ymax

xout,yout,pts=[],[],[]

ndo,xout,yout,pts=ellipsemaker_XY(x0,y0,x1,y1,x2,y2,0,360,36,0)

canvas.create_polygon(pts,width=2,fill='red')。

Function ellipsemaker_XY() can draw inclined ellipse also.

利用python canvas_create_oval(xmin,ymin,xmax,ymax)和自訂函數

ndo,xout,yout,pts=ellipsemaker_XY(x0,y0,x1,y1,x2,y2,0,360,36,0)

者相當，此處

xout,yout,pts=[],[],[]

x0,y0=xmin,(ymin+ymax)/2

x1,y1=xmax,(ymin+ymax)/2

x2,y2=(xmin+xmax)/2,ymax

但ellipsemaker_XY()可以繪製傾斜橢圓及橢圓弧。

---------------------------------------

 (3)Edit of ellipse :

The edit of ellipse curve such as rotation, reflection, offset , tangential line, copy(ring copy), segmental slice of ellipse by means of python tkinter are difficult and complex ,but using user define function  are quite simple and easy. To fill or flood fill an irregular region on PictureBox of vb 6 or vb net are simple and fast. But in Python canvas shapes are difficult and tedious even on image。I try to build a region passing through the boundary key points of the interesting zone (surrounded by ellipse, or circle and lines) ,then fill a predefined pattern or self defined pattern ) by python polygon “stipple” and “fill” method.(stipple=’hourglass’,stipple=’gray50,stipple=’@penginns.xbm’(user_definned xbm file))。To implement this method, You need to find out the segments of the connecting points, firstly. Here, I pose some useful source code to get the ellipse segment to share with people who is interesting.

Vb 6及net可以利用API函數直接在繪圖方塊(PictureBox)上不規則之封閉區域Floodfill及鋪貼圖案，但Python canvas似乎並不直接支援此方法?好像只能在image上操作，因此本人嘗試計算不規則區域之邊界交點及曲線線段，然後與其他線段。理論上應該可行？

def  EllipseReflct(x0,y0,x1,y1,x2,y2,angbeg,angend,npt,xbase0,ybase0

,xbase1,ybase1):

    xout=[]

    yout=[]

    pts=[]

    npt,xout,yout,pts,cenx,ceny=ellipsemaker_XY(x0,y0,x1,y1,x2,y2,angbeg,angend,npt,cenReturn=1)

    xreflcts=[]

    yreflcts=[]

    for i in range(npt):

        bol,xvert,yvert,xreftpt,yreftpt=NearPt_ReflctPt(xout[i],yout[i],xbase0,ybase0,xbase1,ybase1)

        xreflcts.append(xreftpt)

        yreflcts.append(yreftpt)

    return npt,xreflcts,yreflcts

def EllipseRot(x0,y0,x1,y1,x2,y2,angbeg,angend,npt,xRotAt,yRotAt

,angRotIn):

    xout=[]

    yout=[]

    pts=[]

    npt,xout,yout,pts,cenx,ceny=ellipsemaker_XY(x0,y0,x1,y1,x2,y2,angbeg,angend,npt,cenReturn=1)

    xrots=[]

    yrots=[]

    pts=[]

    for i in range(npt):

        xrtpt,yrtpt=RotatePoint(xout[i],yout[i],xRotAt,yRotAt,angRotIn)

        xrots.append(xrtpt)

        yrots.append(yrtpt)

    xcenrot,ycenrot=RotatePoint(cenx,ceny,xRotAt,yRotAt,angRotIn)

    return npt,xrots,yrots,xcenrot,ycenrot

def Offset_In_Out(x0,y0,x1,y1,x2,y2,angbeg,angend,npt,Offset,

isInsideOff=True ):

    #print('in offset')

    #x0=self.x0

    #y0=self.y0

    #x1=self.x1

    #y1=self.y1

    xcen,ycen,aa,bb,angslop=ellipse_Prop(x0,y0,x1,y1,x2,y2)

    print('aa,bb',aa,bb)

    xvert,yvert=ellPoint_byGivenAngle(x0,y0,x1,y1,x2,y2,90)

    print('xvert,yvert',xvert,yvert)

    ll=math.sqrt((xvert-xcen)**2+(yvert-ycen)**2)

    raa=aa

    rbb=bb

    if isInsideOff==True :

        ratpt=(aa-Offset)

        rbtpt=(bb-Offset)

        x0new=xcen+(x0-xcen)*ratpt/raa

        y0new=ycen+(y0-ycen)*ratpt/raa

        x1new=xcen+(x1-xcen)*ratpt/raa

        y1new=ycen+(y1-ycen)*ratpt/raa

        x2new=xcen+(xvert-xcen) *rbtpt/rbb

        y2new=ycen+(yvert-ycen) *rbtpt/rbb

    else:

        ratpt=(aa+Offset)

        rbtpt=(bb+Offset)

        x0new=xcen+(x0-xcen)*ratpt/raa

        y0new=ycen+(y0-ycen)*ratpt/raa

        x1new=xcen+(x1-xcen)*ratpt/raa

        y1new=ycen+(y1-ycen)*ratpt/raa

x2new=xcen+(xvert-xcen) *rbtpt/rbb

        y2new=ycen+(yvert-ycen) *rbtpt/rbb

    xoffsets=[]

    yoffsets=[]

    pts=[]

    npt,xoffsets,yoffsets,pts=ellipsemaker_XY(x0new,y0new,x1new,y1new,x2new,y2new,angbeg,angend,npt,0)

    #xoffset,yoffset=Ellip.Ellipse()

    #print('xoffsets',xoffsets)

    #print('yffsets',yoffsets)

    return npt,xoffsets,yoffsets

def Ellipse2Tans(x0,y0,x1,y1,x2,y2,PtGivenX,PtGivenY):

    EllpCenX,EllpCenY,AA,BB,angslop=ellipse_Prop(x0,y0,x1,y1,x2,y2)

    ptAns1X = 99999.0

    ptAns1Y = 99999.0

    ptAns2X = 99999.0

    ptAns2Y = 99999.0

    Angslop=math.radians(angslop)

    Ta = AA ** 2 * math.sin(Angslop ) **2 + BB ** 2 * math.cos(Angslop ) ** 2

    Tb = AA ** 2 * math.cos(Angslop ) ** 2 + BB ** 2 * math.sin(Angslop) ** 2

    Tc = 2 * math.sin(Angslop ) * math.cos(Angslop) * (BB** 2 - AA ** 2)

    Td = AA **2 * BB **2

    Te = EllpCenX - PtGivenX

    Tf = EllpCenY - PtGivenY

    T1 = 2.0 * Ta * Te + Tc * Tf

    T2 = Tc * Te + 2.0 * Tb * Tf

    T3 = -(Tb * T1 - Tc * T2) / Ta / T1

    T4 = 2 * Tc * Td / Ta / T1

    T5 = Td / Ta

    T6 = -T2 / T1

    T7 = -2.0 * Td / T1

    Fa = T6 ** 2 - T3

    Fb = 2 * T6 * T7 - T4

    Fc = T7 ** 2 - T5

    tpt = Fb ** 2 - 4.0 * Fa * Fc

    print('tpt=',tpt)

    if tpt <= 0.0 :

        print('no solution for Ellipse Tangent line')

        return 'no solution'

    else:

        ptAns1Y = (-Fb - math.sqrt(tpt)) / 2.0 / Fa

        ptAns2Y = (-Fb + math.sqrt(tpt)) / 2.0 / Fa

        ptAns1X = T6 * ptAns1Y + T7

        ptAns2X = T6 * ptAns2Y + T7

        ptAns1X = ptAns1X + EllpCenX  #   平移

        ptAns1Y = ptAns1Y + EllpCenY  #  平移

        ptAns2X = ptAns2X + EllpCenX

        ptAns2Y = ptAns2Y + EllpCenY

        pttans0X = ptAns1X

def ellSlicesbyMile(xxin,yyin,x0,y0,x1,y1,x2,y2,angbeg,angend,npt):

    xout=[]

    yout=[]

    pts=[]

    npt,xout,yout,pts=ellipsemaker_XY(x0,y0,x1,y1,x2,y2,angbeg,angend,npt)

    miles=[]

    xcen,ycen,miles=Milelinexy_cen(xout,yout,1)

    print('in ellSlicesbyMile ^^miles',miles)

    xxonEll=[]

    yyonEll=[]

    xxonEll.append(xout[0]) # add the first point of ellipse

    yyonEll.append(yout[0])

    for i in range(len(xxin)):

        nint,ptonEllipx,ptonEllipy,tAng=point_onEllipse_Angle(xxin[i],yyin[i],x0,y0,x1,y1,x2,y2,angbeg,angend,npt)

        if nint==1:

            xxonEll.append(ptonEllipx)

            yyonEll.append(ptonEllipy)

    xxonEll.append(xout[-1])# add the last point of ellipse

    yyonEll.append(yout[-1])

    milesAns=[]

    milesAns.append(miles[0]) # add the first mile of ellipse

    for i in range(len(xxonEll)):

        yesorno,miletpt=MilesEllipse_givenXy(xxonEll[i],yyonEll[i],xout,yout)

        if yesorno==1:

            milesAns.append(miletpt)

    milesAns.append(miles[-1]) # add the last mile of ellipse

    print('in ellSlicesbyMile milesAns',milesAns)

    xysegAll=[]

    nbeg=0

    for i in range(len(xxonEll)-1):

        xyseg=[]

        xyseg.append([xxonEll[i],yyonEll[i]])  #first point of segment

        for j in range(len(xout)-1):

            if miles[j]>=milesAns[i] and miles[j]>=milesAns[i+1]:

                xyseg.append([xout[j],yout[j]])

        xyseg.append([xxonEll[i+1],yyonEll[i+1]]) #last point of segment

        xysegAll.append(xyseg)

    return xxonEll,yyonEll,xysegAll

        pttans0Y = ptAns1Y

        pttans1X = ptAns2X

        pttans1Y = ptAns2Y

        Ellipse2Tans = 1

        Ltans0 = math.sqrt((pttans0X - PtGivenX) ** 2 + (pttans0Y - PtGivenY) ** 2)

        Ltans1 = math.sqrt((pttans1X - PtGivenX) ** 2 + (pttans1Y - PtGivenY) ** 2)

        return  pttans0X,pttans0Y,pttans1X,pttans1Y,Ltans0,Ltans1

                       <to be continued.>